题目内容
(1) 已知函数 ,求函数
,求函数 的最小值;
的最小值;
(2) 设x,y为正数, 且x+y=1,求 +
+ 的最小值.
的最小值.
(Ⅰ)  ;(Ⅱ)9,当且仅当
;(Ⅱ)9,当且仅当 时等号成立。
时等号成立。
解析试题分析:(1)由于已知中函数变量为大于零,则符合一正,积为定值,故可以考虑运用均值不等式来求解最值。
(2)利用和为定值,将所求解的表达式 +
+ 构造为均值不等式的特点进而求解得到。
构造为均值不等式的特点进而求解得到。
解(Ⅰ)  则由均值不等式可知,
则由均值不等式可知, ,当且仅当
,当且仅当 时等号成立,解得
时等号成立,解得
(Ⅱ) 因为对x,y为正数, 且x+y=1,则 +
+ =(
=( +
+ )(x+y)=5+
)(x+y)=5+ ,当且仅当
,当且仅当 时等号成立。考点:本试题主要考查了均值不等式的求解最值问题。
时等号成立。考点:本试题主要考查了均值不等式的求解最值问题。
点评:解决该试题的关键是运用一正二定三相等来确定是否有最值。

练习册系列答案
相关题目
设变量x,y满足约束条件 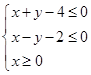 ,则目标函数z=
,则目标函数z=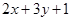 的最大值为
的最大值为
| A.11 | B.10 | C.9. | D.13 |
设变量x,y满足约束条件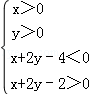 ,则目标函数z=x2+y2的取值范围是( )
,则目标函数z=x2+y2的取值范围是( )
A. | B.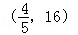 | C.( 1 , 16 ) | D. |
已知实数x,y满足 ,则z=4x+y的最大值为( )
,则z=4x+y的最大值为( )
| A.10 | B.8 |
| C.2 | D.0 |
若变量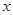 、
、 满足约束条件
满足约束条件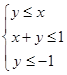 ,且
,且 的最大值和最小值分别为
的最大值和最小值分别为 和
和 ,则
,则 ( )
( )
A.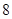 | B.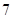 | C. | D. |
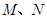 为圆
为圆 与
与 轴的两个交点.
轴的两个交点. 的方程;
的方程;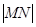 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;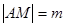 ,
, ,求
,求 的最大值.
的最大值. ,
, ; (2)求
; (2)求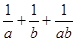 的最小值.
的最小值. 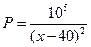 ,若要使每天获得的
,若要使每天获得的 利润最多,销售价格每件应定为多少元
利润最多,销售价格每件应定为多少元 ?
?