已知∠BOC在平面内.OA是平面的斜线.且∠AOB=∠AOC=60°.OA=OB=OC=a.BC=a.求OA与平面所成的角．题目和参考答案——青夏教育精英家教网——

题目内容

(10分) 已知∠BOC在平面

内，OA是平面

的斜线，且∠AOB=∠AOC=60°，OA=OB=OC=a，BC=

a，求OA与平面

所成的角．

45⁰

解析:

设AD⊥平面OBC,垂足为D,OA与平面OBC所成的角为，

∵∠AOB=∠AOC=60°，∴点A在平面OBC上的射影在∠BOC的角平分线上。

∵OB=OC=a，BC=a ∴∠BOD=45⁰ 由三余弦公式，cos∠AOC=cos.cos∠BOD,

cos= cos∠AOC/ cos∠BOD= ∵0⁰<<90⁰ ∴=45⁰ OA与平面OBC所成的角为45⁰.

练习册系列答案

全能好卷系列答案

课课练活页卷系列答案

满分试卷期末冲刺100分系列答案

课程标准同步导练系列答案

新经典练与测系列答案

本土教辅名校学案小学生之友系列答案

全优期末真题8套系列答案

期末好卷系列答案

红领巾乐园系列答案

初中英语最佳方案冲刺AB卷系列答案

相关题目

（2013•宿迁一模）【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，已知AB，CD是圆O的两条弦，且AB是线段CD的垂直平分线，若AB=6，CD=2

，求线段AC的长度．
B．选修4-2：矩阵与变换（本小题满分10分）
已知矩阵M=

2	1
1	a

的一个特征值是3，求直线x-2y-3=0在M作用下的新直线方程．
C．选修4-4：坐标系与参数方程（本小题满分10分）
在平面直角坐标系xOy中，已知曲线C的参数方程是

（α是参数），若以O为极点，x轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线C的极坐标方程．
D．选修4-5：不等式选讲（本小题满分10分）
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R，求正实数a的取值范围．

本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
（1）、选修4-1：几何证明选讲
如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C．求证：BT平分∠OBA
（2）选修4-2：矩阵与变换（本小题满分10分）
若点A（2，2）在矩阵M=

cosα	-sinα
sinα	cosα

对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵
（3）选修4-2：矩阵与变换（本小题满分10分）
在极坐标系中，A为曲线ρ²+2ρcosθ-3=0上的动点，B为直线ρcosθ+ρsinθ-7=0上的动点，求AB的最小值．
（4）选修4-5：不等式选讲（本小题满分10分）
已知a₁，a₂…a_n都是正数，且a₁•a₂…a_n=1，求证：（2+a₁）（2+a₂）…（2+a_n）≥3ⁿ．

（本小题满分10分）

已知B ,C分别为函数y=Asinωx 在y轴右侧的第一个最大值点和最小值

点，O为原点，若 ,且

(1) 求A ， ω 的值

（2）求函数y=Asinωx 的单调递增区间

(本小题满分10分）

已知直线l经过点P（，1），倾斜角，在极坐标系下，圆C的极坐标方程为。

（1）写出直线l的参数方程，并把圆C的方程化为直角坐标方程；

（2）设l与圆C相交于A，B两点，求点P到A，B两点的距离之积。

（本小题满分10分）

已知向量设函数

（1）求的最小正周期与单调递减区间；

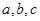（2）在△ABC中分别是角A、B、C的对边，若△ABC的面积为，求的值.