题目内容
已知平面向量的集合A到B的映射f为f(
)=
-2(
•
)
,其中
为常向量,若映射f满足f(
)•f(
)=
•
对任意
,
∈A恒成立,则
用坐标可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
分析:通过赋值列出关于向量的方程,通过向量的运算法则化简方程,得到
满足的条件.
| a |
解答:解:令
=
,则
f(
)•f(
)=
•
又f(
)•f(
)
=[
-2(
•
)
]2
=
2-4(
•
)2+4[(
•
)
]2
即-4(
•
)2+4[(
•
)
]2=0,
∴(
•
)2(
2-1)=0
∴
=0或|
|=1,
对于选项D,|(-
,
)|=1,
故选D.
| y |
| x |
f(
| x |
| x |
| x |
| x |
又f(
| x |
| x |
=[
| x |
| x |
| a |
| a |
=
| x |
| x |
| a |
| x |
| a |
| a |
即-4(
| x |
| a |
| x |
| a |
| a |
∴(
| x |
| a |
| a |
∴
| a |
| a |
对于选项D,|(-
| 1 |
| 2 |
| ||
| 2 |
故选D.
点评:本题考查向量的运算法则及向量的运算律.属于基础题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 )=
)= )
) )=
)=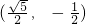
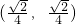
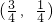
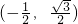
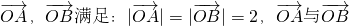 的夹角为
的夹角为 ,又
,又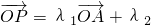
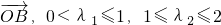 ,则点P的集合所表示的图形面积为
,则点P的集合所表示的图形面积为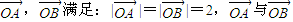 的夹角为
的夹角为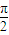 ,又
,又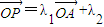
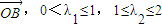 ,则点P的集合所表示的图形面积为( )
,则点P的集合所表示的图形面积为( )