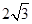题目内容
已知平面向量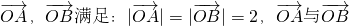 的夹角为
的夹角为 ,又
,又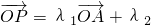
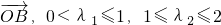 ,则点P的集合所表示的图形面积为
,则点P的集合所表示的图形面积为
- A.8
- B.4
- C.2
- D.1
B
分析:本题考查的知识点是平面区域的面积,处理的方法是根据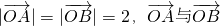 的夹角为
的夹角为 ,及
,及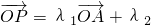
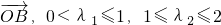 ,构造平面直角坐标系,将满足不等式表示的可行域表示出来,从而将P点对应的图形描述出来,即可求解.
,构造平面直角坐标系,将满足不等式表示的可行域表示出来,从而将P点对应的图形描述出来,即可求解.
解答: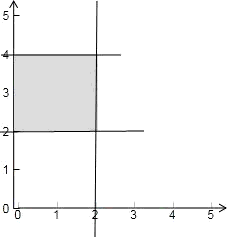 解:∵
解:∵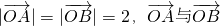 的夹角为
的夹角为
∴不妨以O为原点,以OA方向为x轴正方向,
以OB方向为Y轴正方向建立坐标系
则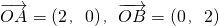
又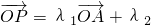
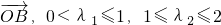
令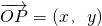
则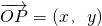 =(2λ1,2λ2)且0<x≤2,2≤y≤4
=(2λ1,2λ2)且0<x≤2,2≤y≤4
其表示的平面区域如下图示:
由图可知阴影部分的面积为4
故选B
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.
分析:本题考查的知识点是平面区域的面积,处理的方法是根据
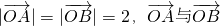 的夹角为
的夹角为 ,及
,及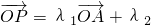
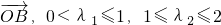 ,构造平面直角坐标系,将满足不等式表示的可行域表示出来,从而将P点对应的图形描述出来,即可求解.
,构造平面直角坐标系,将满足不等式表示的可行域表示出来,从而将P点对应的图形描述出来,即可求解.解答:
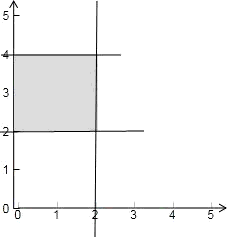 解:∵
解:∵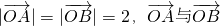 的夹角为
的夹角为
∴不妨以O为原点,以OA方向为x轴正方向,
以OB方向为Y轴正方向建立坐标系
则
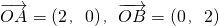
又
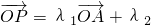
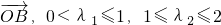
令
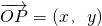
则
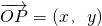 =(2λ1,2λ2)且0<x≤2,2≤y≤4
=(2λ1,2λ2)且0<x≤2,2≤y≤4其表示的平面区域如下图示:
由图可知阴影部分的面积为4
故选B
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

练习册系列答案
相关题目
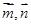 的夹角为
的夹角为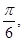 且
且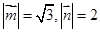 ,在
,在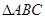 中,
中,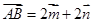 ,
,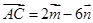 ,
,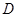 为
为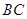 中点,则
中点,则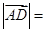 ( )
( )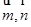 的夹角为
的夹角为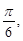 且
且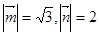 ,在
,在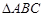 中,
中, ,
,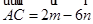 ,
,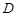 为
为 中点,则
中点,则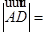 (
)
(
)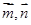 的夹角为
的夹角为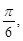 且
且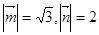 ,在
,在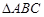 中,
中,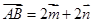 ,
,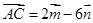 ,
,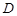 为
为 中点,则
中点,则 ( )
( )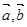 的夹角为
的夹角为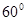 ,
,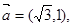
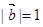 ,则
,则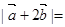
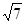 C.
C.
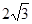 D.
D.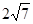
 的夹角为60°,
的夹角为60°, ,
,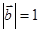 ,则
,则 ( )
( ) B.
B. C.
C.  D.
D.