题目内容
【题目】已知{an}是各项都为正数的等比数列,其前n项和为Sn , 且S2=3,S4=15.
(1)求数列{an}的通项公式;
(2)若数列{bn}是等差数列,且b3=a3 , b5=a5 , 试求数列{bn}的前n项和Mn .
【答案】
(1)解:设等比数列{an}的公比为q,由题意分析知q≠1.
由S2=3,S4=15得: 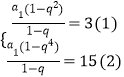 ,
,
![]() 得1+q2=5,得q2=4,由题意q>0,所以q=2.
得1+q2=5,得q2=4,由题意q>0,所以q=2.
将q=2代入(1)式得a1=1,
所以 ![]() .
.
(2)解:设数列{bn}的公差为d,
∵ ![]() ,
,
又{bn}为等差数列,∴b5=b3+(5﹣3)d,
即16=4+2d,解得d=6,
又由b3=b1+(3﹣1)d,得b1=﹣8
∴ ![]()
=3n2﹣11n.
【解析】(1)设等比数列{an}的公比为q,由题意分析知q≠1.运用等比数列的求和公式,解方程可得首项与公比,由等比数列的通项公式即可得到所求;(2)设数列{bn}的公差为d,运用等差数列的通项公式可得公差和首项,运用等差数列的求和公式,进而得到所求和.
【考点精析】利用等比数列的通项公式(及其变式)和数列的前n项和对题目进行判断即可得到答案,需要熟知通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系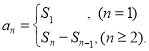 .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表:
原料 | 磷酸盐(单位:吨) | 硝酸盐(单位:吨) |
甲 | 4 | 20 |
乙 | 2 | 20 |
现库存磷酸盐8吨、硝酸盐60吨,计划在此基础上生产若干车皮的甲、乙两种混合肥料.
(1)设x,y分别表示计划生产甲、乙两种肥料的车皮数,试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)若生产1车皮甲种肥料,利润为3万元;生产1车皮乙种肥料,利润为2万元.那么分别生产甲、乙两种肥料多少车皮,能够产生最大利润?最大利润是多少?