题目内容
(1)用综合法或分析法证明: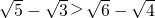
(2)用反证法求证: .
. .
. 三个数不可能成等差数列.
三个数不可能成等差数列.
证明:(1)要证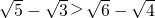 ,只要证
,只要证 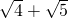 >
>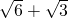 ,
,
只要证 9+2 >9+2
>9+2 ,只要证
,只要证  >
> . 而
. 而  >
> 显然成立,
显然成立,
故原不等式成立.
(2)假设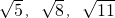 这三个数成等差数列,则由等差数列的性质可得 2
这三个数成等差数列,则由等差数列的性质可得 2 =
=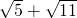 ,
,
∴32=5+11+2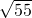 ,∴8=
,∴8=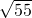 ,∴64=55 (矛盾),故假设不成立,
,∴64=55 (矛盾),故假设不成立,
∴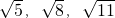 这三个数不可能成等差数列.
这三个数不可能成等差数列.
分析:(1)只要证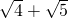 >
>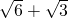 ,只要证 9+2
,只要证 9+2 >9+2
>9+2 ,只要证
,只要证  >
> .
.
(2)假设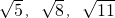 这三个数成等差数列,则有 2
这三个数成等差数列,则有 2 =
=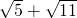 ,能推出64=55 (矛盾 ).
,能推出64=55 (矛盾 ).
点评:本题考查用分析法和反证法证明不等式,用分析法证明不等式的关键是寻找使不等式成立的充分条件,用反证法证明不等式的关键是推出矛盾.
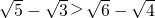 ,只要证
,只要证 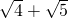 >
>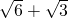 ,
,只要证 9+2
 >9+2
>9+2 ,只要证
,只要证  >
> . 而
. 而  >
> 显然成立,
显然成立,故原不等式成立.
(2)假设
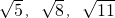 这三个数成等差数列,则由等差数列的性质可得 2
这三个数成等差数列,则由等差数列的性质可得 2 =
=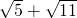 ,
,∴32=5+11+2
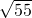 ,∴8=
,∴8=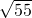 ,∴64=55 (矛盾),故假设不成立,
,∴64=55 (矛盾),故假设不成立,∴
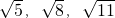 这三个数不可能成等差数列.
这三个数不可能成等差数列.分析:(1)只要证
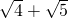 >
>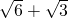 ,只要证 9+2
,只要证 9+2 >9+2
>9+2 ,只要证
,只要证  >
> .
.(2)假设
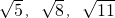 这三个数成等差数列,则有 2
这三个数成等差数列,则有 2 =
=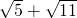 ,能推出64=55 (矛盾 ).
,能推出64=55 (矛盾 ).点评:本题考查用分析法和反证法证明不等式,用分析法证明不等式的关键是寻找使不等式成立的充分条件,用反证法证明不等式的关键是推出矛盾.

练习册系列答案
相关题目

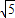 .
.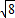 .
.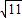 三个数不可能成等差数列.
三个数不可能成等差数列.