题目内容
已知α+β=| π | 2 |
分析:本题的关键是把2α+β和α+2β巧妙地分成α+(α+β)和(α+β)+β,就可以利用诱导公式解决了.
解答:证明:∵sin(2α+β)tanα+cos(α+2β)cotβ
=sin(α+α+β)tanα+cos(α+α+β)cotβ
=cosα
-sinβ
=sinα-cosβ
又∵α+β=
∴sinα-cosβ=sinα-sin(
-α)=sinα-sinα=0
=sin(α+α+β)tanα+cos(α+α+β)cotβ
=cosα
| sinα |
| cosα |
| cosβ |
| sinβ |
又∵α+β=
| π |
| 2 |
∴sinα-cosβ=sinα-sin(
| π |
| 2 |
点评:本题主要考查了诱导公式的运用.属基础题.

练习册系列答案
相关题目
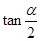 =2,求 (I)
=2,求 (I)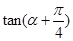 的值; (2)
的值; (2)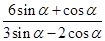 的值.
的值. =2,求 :
=2,求 :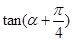 的值; (2)
的值; (2) 的值.
的值.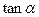 =2,求:
=2,求: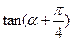 的值; (2)
的值; (2) 的值.
的值.