题目内容
已知2α+β=π,求y=cosβ-6sinα的最小值及最大值.
分析:由2α+β=π⇒β=π-2α,从而可得y=2sin2α-6sinα-1,配方整理即可求原式的最小值及最大值.
解答:解:∵2α+β=π,
∴β=π-2α,
∴y=2sin2α-6sinα-1=2(sinα-
)2-
,
令t=sinα,则|t|≤1,
∴y=2(t-
)2-
,
∵其对称轴为t=
,
∴当t=-1时,ymax=7,
当t=1时,ymin=-5.
∴β=π-2α,
∴y=2sin2α-6sinα-1=2(sinα-
| 3 |
| 2 |
| 11 |
| 2 |
令t=sinα,则|t|≤1,
∴y=2(t-
| 3 |
| 2 |
| 11 |
| 2 |
∵其对称轴为t=
| 3 |
| 2 |
∴当t=-1时,ymax=7,
当t=1时,ymin=-5.
点评:本题考查三角函数的最值,考查二次函数的配方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
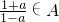 ,请考虑以下问题:
,请考虑以下问题: