题目内容
已知2α+β=π,求y=cosβ-6sinα的最大值分析:先由:2α+β=π,结合配方法将y=cos(π-2α)-6siα转化为:y=2(sinα-
)2-
,再令t=sinα∈[-1,1],用二次函数的性质求解.
| 3 |
| 2 |
| 11 |
| 2 |
解答:解:∵2α+β=π,
y=cos(π-2α)-6siα=-cos2α-6sinα=2(sinα)2-6sinα-1=2(sinα-
)2-
,
令t=sinα∈[-1,1],
∴当t=-1时取得最大值7,
当t=1时取得最小值-5,
故答案为:7,-5.
y=cos(π-2α)-6siα=-cos2α-6sinα=2(sinα)2-6sinα-1=2(sinα-
| 3 |
| 2 |
| 11 |
| 2 |
令t=sinα∈[-1,1],
∴当t=-1时取得最大值7,
当t=1时取得最小值-5,
故答案为:7,-5.
点评:本题主要考查角的变换及倍角公式在转化函数中的应用,一般来讲考查函数的性质时要转化为基本函数求解.

练习册系列答案
相关题目
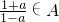 ,请考虑以下问题:
,请考虑以下问题: