题目内容
如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C.
(I)求证:当b变化时,圆C的圆心在一条定直线上;
(II)求证:圆C经过除原点外的一个定点;
(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?
(I)求证:当b变化时,圆C的圆心在一条定直线上;
(II)求证:圆C经过除原点外的一个定点;
(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?

解:(I)在方程y=x2+bx中.
令y=0,y=x,易得A(﹣b,0),B(1﹣b,1﹣b)
设圆C的方程为x2+y2+Dx+Ey=0,则
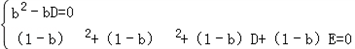
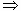
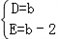 ,
,
故经过三点O,A,B的圆C的方程为
x2+y2+bx+(b﹣2)y=0,
设圆C的圆心坐标为(x0,y0),则
x0=﹣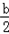 ,y0=﹣
,y0=﹣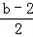 ,
,
∴y0=x0+1,这说明当b变化时,
(I)中的圆C的圆心在定直线y=x+1上.
(II)设圆C过定点(m,n),则m2+n2+bm+(b﹣2)n=0,整理得
(m+n)b+m2+n2﹣2n=0,它对任意b≠0恒成立,
∴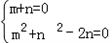
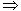
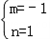 或
或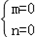
故当b变化时,(I)中的圆C经过除原点外的一个定点坐标为(﹣1,1).
(III)抛物线M的顶点坐标为(﹣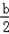 ,﹣
,﹣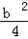 ),
),
若存在这样的抛物线M,使它的顶点与它对应的圆C的圆心之间的距离不大于圆C的半径,则
|﹣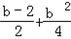 |≤
|≤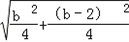 ,
,
整理得(b2﹣2b)2≤0,
因b≠0,∴b=2,
以上过程均可逆,
故存在抛物线M:y=x2+2x,使它的顶点与C的距离不大于圆C的半径.
令y=0,y=x,易得A(﹣b,0),B(1﹣b,1﹣b)
设圆C的方程为x2+y2+Dx+Ey=0,则
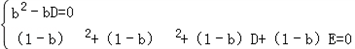
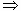
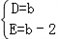 ,
,故经过三点O,A,B的圆C的方程为
x2+y2+bx+(b﹣2)y=0,
设圆C的圆心坐标为(x0,y0),则
x0=﹣
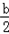 ,y0=﹣
,y0=﹣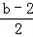 ,
,∴y0=x0+1,这说明当b变化时,
(I)中的圆C的圆心在定直线y=x+1上.
(II)设圆C过定点(m,n),则m2+n2+bm+(b﹣2)n=0,整理得
(m+n)b+m2+n2﹣2n=0,它对任意b≠0恒成立,
∴
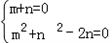
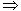
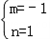 或
或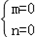
故当b变化时,(I)中的圆C经过除原点外的一个定点坐标为(﹣1,1).
(III)抛物线M的顶点坐标为(﹣
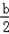 ,﹣
,﹣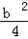 ),
),若存在这样的抛物线M,使它的顶点与它对应的圆C的圆心之间的距离不大于圆C的半径,则
|﹣
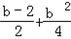 |≤
|≤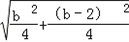 ,
,整理得(b2﹣2b)2≤0,
因b≠0,∴b=2,
以上过程均可逆,
故存在抛物线M:y=x2+2x,使它的顶点与C的距离不大于圆C的半径.

练习册系列答案
相关题目
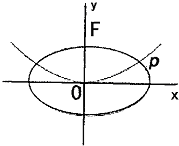 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: 如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C.
如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C. 如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C.
如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C.