题目内容
已知函数f(x)=x3+ax2+bx+c。当x=-1时,函数取得极大值7;当x=3时,函数取得极小值。求a、b、 c、及函数的极小值。
答案:
解析:
解析:
解:∵ f(x)=x3+ax2+bx+c,∴ f′(x)=3x3+2ax2+b 由题意得x=-1、x=3是方程3x3+2ax2+b=0的根, ∴ ∴ -1+a-b+c=7。∴ c=2。 ∴ f(x)=x3-3x2-9x+2。∴ f(3)=33-3×32-9×3+2=-25。 ∴ a=-3,b=-9,c=2。 当x=3时函数取得极小值-25。
|

练习册系列答案
相关题目
 ,其中
,其中 表示函数f(x)在
表示函数f(x)在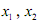 ,且
,且 ,证明:
,证明: 

 ,且f(1)=2.
,且f(1)=2. R,则下列各式成立的是
R,则下列各式成立的是