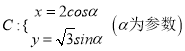题目内容
【题目】已知数列满足:a1=1,an+1= ![]() ,(n∈N*),若bn+1=(n﹣λ)(
,(n∈N*),若bn+1=(n﹣λ)( ![]() +1),b1=﹣λ,且数列{bn}是单调递增数列,则实数λ的取值范围为 .
+1),b1=﹣λ,且数列{bn}是单调递增数列,则实数λ的取值范围为 .
【答案】λ<2
【解析】解:∵数列{an}满足:a1=1,an+1= ![]() ,(n∈N*), ∴
,(n∈N*), ∴ ![]() ,化为
,化为 ![]() ,
,
∴数列 ![]() 是等比数列,首项为
是等比数列,首项为 ![]() +1=2,公比为2,
+1=2,公比为2,
∴ ![]() ,
,
∴bn+1=(n﹣λ)( ![]() +1)=(n﹣λ)2n ,
+1)=(n﹣λ)2n ,
∵b1=﹣λ,且数列{bn}是单调递增数列,
∴bn+1>bn ,
∴(n﹣λ)2n>(n﹣1﹣λ)2n﹣1 ,
化为λ<n+1,
∵数列{n+1}为单调递增数列,
∴λ<2.
∴实数λ的取值范围为λ<2.
所以答案是:λ<2.
【考点精析】解答此题的关键在于理解数列的通项公式的相关知识,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
相关题目