题目内容
对于实数x,将满足“0≤y<1且x-y为整数”的实数y称为实数x的小数部分,用记号<x>表示.对于实数a,无穷数列{an}满足如下条件:( i )a1=<a>;(ii)an+1=
,当a>
时,对任意的自然数n都有an=a,则实数a= .
|
| 1 |
| 2 |
分析:由a1=<a>=a,a>
,可得
<a<1,从而a1=<
>=<
>=
-1=a,即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
解答:解:∵a1=<a>=a,a>
,
∴
<a<1,
∴1<
<2,
∴a1=<
>=<
>=
-1=a
∴a2+a-1=0
解得:a=
,(a=
∉(
,1)舍去)
故答案为:
.
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴1<
| 1 |
| a |
∴a1=<
| 1 |
| a1 |
| 1 |
| a |
| 1 |
| a |
∴a2+a-1=0
解得:a=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
| 1 |
| 2 |
故答案为:
-1+
| ||
| 2 |
点评:本题考查数列递推式,考查新定义,考查学生的计算能力,属于基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
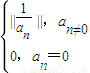 其中n=1,2,3,…
其中n=1,2,3,…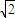 ,求数列{an};
,求数列{an};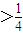 时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A.
时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A.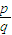 (p 是整数,q是正整数,p、q互质),问对于大于q的任意正整数n,是否都有an=0成立,并证明你的结论.
(p 是整数,q是正整数,p、q互质),问对于大于q的任意正整数n,是否都有an=0成立,并证明你的结论.