Question

（本小题满分10分）选修4－1：几何证明选讲

如图，已知AP是⊙O的切线，P为切点，AC是⊙O的割线，与⊙O交于B、C两点，圆心O在的内部，点M是BC的中点.

（Ⅰ）证明A，P，O，M四点共圆；

（Ⅱ）求∠OAM＋∠APM的大小.

 

 

 

 

Answer 1

【答案】

（Ⅰ）A，P，O，M四点共圆

（Ⅱ）∠OAM＋∠APM=90°

【解析】（Ⅰ）证明：连结OP，OM.

因为AP与⊙O相切于点P，所以

OP⊥AP.

因为M是⊙O的弦BC的中点，所以

OM⊥BC.

于是∠OPA＋∠OMA=180°，由圆心O在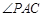的内部，可知四边形APOM的对角互补，所以A，P，O，M四点共圆.                                 ……6分

（Ⅱ）解：由（Ⅰ）得A，P，O，M四点共圆，所以

∠OAM=∠OPM.

由（Ⅰ）得OP⊥AP.

由圆心O在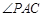的内部，可知∠OPM＋∠APM=90°.

所以∠OAM＋∠APM=90°.                                     ……10分