题目内容
(本小题满分10分)选修4-5:不等式选讲
设函数 ,其中
,其中 .
.
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式 的解集为
的解集为 ,求a的值.
,求a的值.
设函数
 ,其中
,其中 .
.(Ⅰ)当
 时,求不等式
时,求不等式 的解集;
的解集;(Ⅱ)若不等式
 的解集为
的解集为 ,求a的值.
,求a的值.(Ⅰ) 或
或 . (Ⅱ)
. (Ⅱ)  。
。
 或
或 . (Ⅱ)
. (Ⅱ)  。
。(I)当a=1时,不等式转化为 ,此不等式易解.
,此不等式易解.
(II)解本小题关键是把 转化为
转化为 ,然后再讨论去绝对值转化为
,然后再讨论去绝对值转化为 或
或 即
即 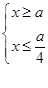 或
或
求解.
解:(Ⅰ)当 时,
时, 可化为
可化为 .
.
由此可得 或
或 .故不等式
.故不等式 的解集为
的解集为
 或
或 .……………… 5分
.……………… 5分
(Ⅱ) 由 得
得  ,此不等式化为不等式组
,此不等式化为不等式组
 或
或 即
即 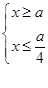 或
或
因为 ,所以不等式组的解集为
,所以不等式组的解集为 由题设可得
由题设可得 =
=  ,
,
故 …… 10分
…… 10分
 ,此不等式易解.
,此不等式易解.(II)解本小题关键是把
 转化为
转化为 ,然后再讨论去绝对值转化为
,然后再讨论去绝对值转化为 或
或 即
即 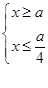 或
或
求解.
解:(Ⅰ)当
 时,
时, 可化为
可化为 .
.由此可得
 或
或 .故不等式
.故不等式 的解集为
的解集为 或
或 .……………… 5分
.……………… 5分(Ⅱ) 由
 得
得  ,此不等式化为不等式组
,此不等式化为不等式组 或
或 即
即 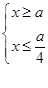 或
或
因为
 ,所以不等式组的解集为
,所以不等式组的解集为 由题设可得
由题设可得 =
=  ,
,故
 …… 10分
…… 10分
练习册系列答案
相关题目
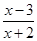 <0的解集为( )
<0的解集为( )


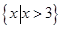
 ,求证:
,求证: 。
。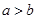 且
且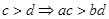 ②
②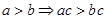
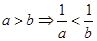 ④
④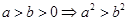
 下列不等式成立的是 ( )
下列不等式成立的是 ( )




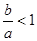


 ,则使得
,则使得 都成立的x取值范围是( )
都成立的x取值范围是( )



 ,则
,则



