题目内容
7.在△ABC中,已知$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{2014}{2015}$,试判断△ABC的形状.分析 方法一、把由余弦定理解出的余弦表达式代入已知的等式化简可得:(a2-b2)c2=(a2-b2)(a2+b2),由a≠b,即可得到结论;
方法二、根据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B,进而推断A=B,或A+B=90°,由a≠b,答案可得.
解答 解法一:由$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{2014}{2015}$,可得
acosA=bcosB(a≠b),
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
∴$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$•a=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$•b,
化简得:a2c2-a4=b2c2-b4,即(a2-b2)c2=(a2-b2)(a2+b2),
由a≠b,则a2+b2=c2,△ABC是直角三角形,
所以△ABC是直角三角形.
解法二:根据正弦定理可知∵acosA=bcosB,
∴sinAcosA=sinBcosB
∴sin2A=sin2B
∴A=B,或2A+2B=180°即A+B=90°,
由a≠b,即A≠B,
所以△ABC为直角三角形.
点评 本题考查三角形的形状的判断,考查正弦定理和余弦定理的运用,考查化简整理的能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.已知A={a,b},B={x|x⊆A},则A与B的关系是( )
| A. | A=B | B. | A⊆B | C. | B⊆A | D. | A∈B |
8.已知$\frac{2}{x}$+$\frac{3}{y}$=2(x>0,y>0),则xy的最小值为( )
| A. | 2 | B. | 6 | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
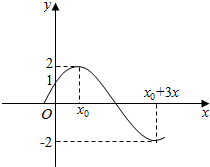 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图 
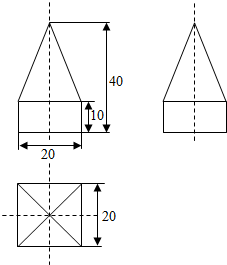 如图所示为一个多面组合体的三视图(单位:cm)
如图所示为一个多面组合体的三视图(单位:cm)