题目内容
【题目】已知数列{an}满足a1=a,an+1=2an+![]() (a,λ∈R).
(a,λ∈R).
(1)若λ=-2,数列{an}单调递增,求实数a的取值范围;
(2)若a=2,试写出an≥2对任意的n∈N*成立的充要条件,并证明你的结论.
【答案】见解析
【解析】(1)当λ=-2时,an+1=2an-![]() ,由题意知an+1>an,所以an+1-an=an-
,由题意知an+1>an,所以an+1-an=an-![]() >0,解得an>
>0,解得an>![]() 或-
或-![]() <an<0,所以a1>
<an<0,所以a1>![]() 或-
或-![]() <a1<0.所以实数a的取值范围为
<a1<0.所以实数a的取值范围为
(-![]() ,0)∪(
,0)∪(![]() ,+∞).
,+∞).
(2)an≥2对任意的n∈N*成立的充要条件为λ≥-4.
证明如下:必要性:假设an+1=2an+![]() ≥2,得λ≥-2a+2an,令f(n)=-2·
≥2,得λ≥-2a+2an,令f(n)=-2·![]()
![]() +
+![]() ,由an≥2,可得f(n)max=-4,即λ≥-4.
,由an≥2,可得f(n)max=-4,即λ≥-4.
充分性:用数学归纳法证明:显然当n=1时,a1≥2成立.
假设当n=k(k≥2)时,ak≥2成立.
当n=k+1时,ak+1=2ak+![]() .
.
令函数f(x)=2x+![]() ,x∈[2,+∞).
,x∈[2,+∞).
①当-4≤λ≤0时,由f′(x)=2-![]() >0,知f(x)在区间[2,+∞)上单调递增,所以ak+1=2ak+
>0,知f(x)在区间[2,+∞)上单调递增,所以ak+1=2ak+![]() ≥4+
≥4+![]() ≥2.
≥2.
②当λ>0时,对x∈[2,+∞)总有f(x)=2x+![]() >4>2,所以ak+1=2ak+
>4>2,所以ak+1=2ak+![]() >2.
>2.
所以当n=k+1时,ak+1≥2成立.
综上可知,当λ≥-4时,对任意的n∈N*,an≥2成立.
故an≥2对任意的n∈N*成立的充要条件是λ≥-4.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).如图茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
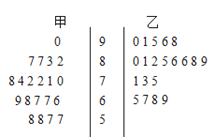
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀,请填写![]() 列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式与临界值表: 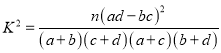 .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |