题目内容
在△ABC中，三边a、b、c成等差数列，则角B的取值范围是________．
（0，
]
分析：设出三角形的三边分别为a，b，c，由三边成等差数列，利用等差数列的性质可知2b=a+c，利用余弦定理表示出cosB，然后把b=
（a+c）代入，利用基本不等式即可求出cosB的最小值，根据B的范围及余弦函数在此区间为减函数即可得到B的范围
解答：设三角形的三边分别为a，b，c，
∵三边成等差数列，∴b=
，
∴cosB=
=
=
≥
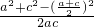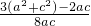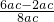=，当且仅当a=c时取等号，
又B∈（0，π），且余弦函数在此区间为减函数，
则B∈（0，
]．
故答案为：（0，]
点评：此题属于解三角形的题型，涉及的知识有：余弦定理，等差数列的性质，基本不等式，以及余弦函数的图象与性质，熟练掌握定理及性质是解本题的关键．
]分析：设出三角形的三边分别为a，b，c，由三边成等差数列，利用等差数列的性质可知2b=a+c，利用余弦定理表示出cosB，然后把b=
（a+c）代入，利用基本不等式即可求出cosB的最小值，根据B的范围及余弦函数在此区间为减函数即可得到B的范围解答：设三角形的三边分别为a，b，c，
∵三边成等差数列，∴b=
，∴cosB=
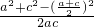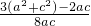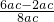==≥=，当且仅当a=c时取等号，又B∈（0，π），且余弦函数在此区间为减函数，
则B∈（0，
]．故答案为：（0，
]点评：此题属于解三角形的题型，涉及的知识有：余弦定理，等差数列的性质，基本不等式，以及余弦函数的图象与性质，熟练掌握定理及性质是解本题的关键．
练习册系列答案
相关题目
在△ABC中，三边a、b、c与面积S的关系是S=
（a2+b2-c2），则角C应为（ ）
| 1 |
| 4 |
| A、30° | B、45° |
| C、60° | D、90° |