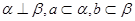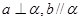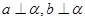题目内容
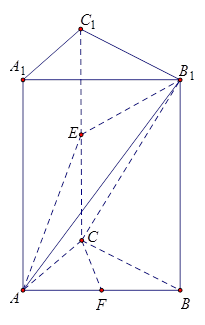
(本小题满分12分)如图:在三棱锥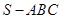 中,已知点
中,已知点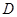 、
、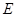 、
、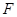 分别为棱
分别为棱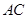 、
、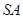 、
、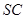 的中点.
的中点.
(1)求证: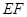 ∥平面
∥平面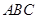 ;
;
(2)若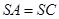 ,
,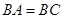 ,求证:平面
,求证:平面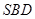 ⊥平面
⊥平面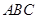 .
.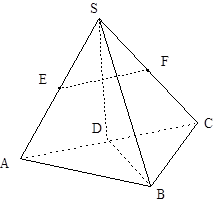
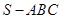 中,已知点
中,已知点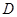 、
、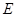 、
、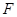 分别为棱
分别为棱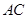 、
、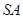 、
、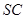 的中点.
的中点.(1)求证:
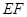 ∥平面
∥平面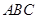 ;
;(2)若
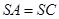 ,
,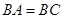 ,求证:平面
,求证:平面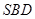 ⊥平面
⊥平面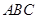 .
.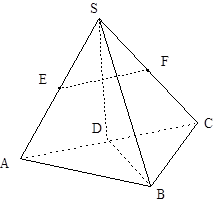
(Ⅰ)见解析;(Ⅱ)见解析。
本题主要考查了直线与平面平行的判定,以及面面的垂直的判定,同时考查空间想象能力、推理论证能力,考查数形结合思想、化归与转化思想,属于基础题.
(Ⅰ)欲证EF∥平面ABC,根据直线与平面平行的判定定理可知只需证EF与平面ABC内一直线平行,而EF是△SAC的中位线,则EF∥AC.又EF?平面ABC,AC?平面ABC,满足定理所需条件;
(Ⅱ)欲证平面SBD⊥平面ABC,根据面面垂直的判定定理可知在平面ABC内一直线与平面SBD垂直,而SD⊥AC,BD⊥AC,又SD∩DB=D,满足线面垂直的判定定理,则AC⊥平面SBD,又AC?平面ABC,从而得到结论
证明:(Ⅰ)∵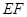 是
是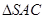 的中位线,∴
的中位线,∴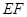 ∥
∥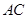 .
.
又∵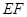
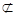 平面
平面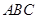 ,
,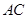
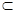 平面
平面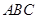 ,∴
,∴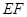 ∥平面
∥平面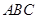
(Ⅱ)∵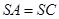 ,
,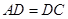 ,∴
,∴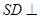
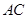 .∵
.∵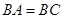 ,
,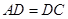 ,∴
,∴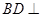
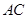 .
.
又∵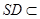 平面
平面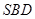 ,
,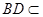 平面
平面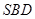 ,
,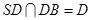 ,∴
,∴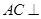 平面
平面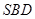 ,
,
又∵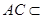 平面
平面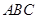 ,∴平面
,∴平面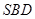
(Ⅰ)欲证EF∥平面ABC,根据直线与平面平行的判定定理可知只需证EF与平面ABC内一直线平行,而EF是△SAC的中位线,则EF∥AC.又EF?平面ABC,AC?平面ABC,满足定理所需条件;
(Ⅱ)欲证平面SBD⊥平面ABC,根据面面垂直的判定定理可知在平面ABC内一直线与平面SBD垂直,而SD⊥AC,BD⊥AC,又SD∩DB=D,满足线面垂直的判定定理,则AC⊥平面SBD,又AC?平面ABC,从而得到结论
证明:(Ⅰ)∵
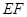 是
是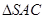 的中位线,∴
的中位线,∴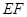 ∥
∥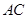 .
.又∵
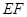
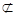 平面
平面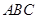 ,
,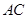
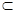 平面
平面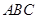 ,∴
,∴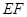 ∥平面
∥平面
(Ⅱ)∵
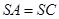 ,
,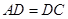 ,∴
,∴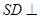
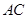 .∵
.∵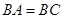 ,
,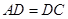 ,∴
,∴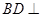
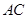 .
.又∵
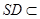 平面
平面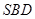 ,
,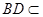 平面
平面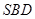 ,
,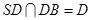 ,∴
,∴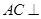 平面
平面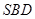 ,
,又∵
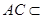 平面
平面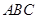 ,∴平面
,∴平面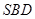

练习册系列答案
相关题目
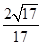 ,若存在,求CE的长,若不存在,请说明理由.
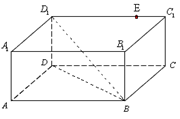
,若存在,求CE的长,若不存在,请说明理由.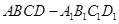 中,底面
中,底面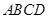 为正方形,
为正方形,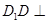 面
面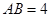 ,
,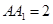 ,点
,点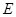 在棱
在棱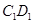 上,且
上,且 .
.
 上确定一点
上确定一点 ,使得直线
,使得直线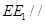 平面
平面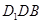 ,并证明;
,并证明;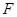 在底面
在底面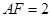 ,请说明点
,请说明点 长度的最小值.
长度的最小值. BE,AB
BE,AB
 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求
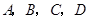 为空间四点.在
为空间四点.在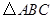 中,
中,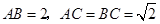 .等边三角形
.等边三角形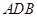 以
以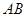 为轴运动.
为轴运动.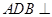 平面
平面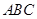 时,求
时,求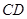 ;
;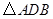 转动时,证明总有
转动时,证明总有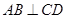 ?
?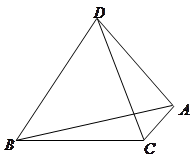
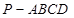 中,底面
中,底面 为平行四边形,
为平行四边形,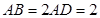 ,
,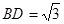 ,
,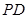 ⊥底面
⊥底面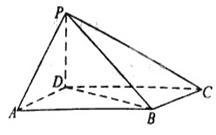
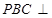 平面
平面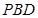 ;
; 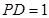 ,求
,求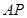 与平面
与平面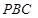 所成角
所成角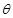 的正弦值.
的正弦值. 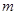 、
、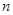 是两条不同的直线,
是两条不同的直线,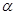 、
、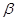 是两个不同的平面,则下面命题中正确的是( )
是两个不同的平面,则下面命题中正确的是( )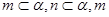 ∥
∥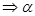 ∥
∥ ,
,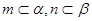
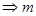 ∥
∥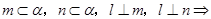
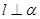
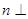
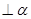
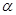 、
、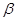 和直线
和直线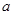 、
、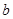 ,若
,若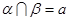 ,
,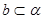 且
且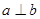 ,则
,则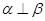 .
.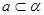 ,
,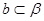 且
且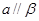 ,
,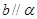 ,则
,则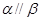 .
.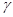 和直线
和直线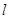 ,若
,若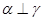 ,
,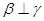 且
且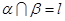 ,则
,则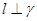 .
.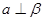 ,则
,则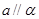 .
.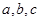 是三条不同的直线,
是三条不同的直线,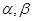 是两个不同的平面,则能使
是两个不同的平面,则能使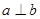 成立是( )
成立是( )