题目内容
【题目】如图,圆![]() 为圆
为圆![]() 上任意一点,过
上任意一点,过![]() 作圆
作圆![]() 的切线,分别交直线
的切线,分别交直线![]() 和
和![]() 于
于![]() 两点,连接
两点,连接![]() ,相交于点
,相交于点![]() ,若点
,若点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)设直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的值,并求曲线
的值,并求曲线![]() 的方程;
的方程;
(2)记直线![]() 与曲线
与曲线![]() 有两个不同的交点
有两个不同的交点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,求
,求![]() 的面积与
的面积与![]() 的面积的比值
的面积的比值![]() 的最大值及取得最大值时
的最大值及取得最大值时![]() 的值.
的值.
(注:![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() )
)

【答案】(1)![]() (
(![]() );(2)
);(2)![]() 取得最大值
取得最大值![]() ,此时
,此时![]() .
.
【解析】
(1)易知过点![]() 的切线方程为
的切线方程为![]() ,其中
,其中![]() ,
,
则![]() ,从而得到
,从而得到![]() ,进而得到曲线
,进而得到曲线![]() 的方程;
的方程;
(2)联立![]() 消去
消去![]() ,得
,得![]() ,利用根与系数的关系得到
,利用根与系数的关系得到![]() ,进而求出
,进而求出![]() ,从而有
,从而有![]() ,利用换元法转化为二次函数的最值问题.
,利用换元法转化为二次函数的最值问题.
(1)易知过点![]() 的切线方程为
的切线方程为![]() ,其中
,其中![]() ,
,
则![]() ,
,
∴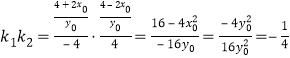
设![]() ,则
,则![]() (
(![]() )
)
故曲线![]() 的方程为
的方程为![]() (
(![]() )
)
(2)联立![]() 消去
消去![]() ,得
,得![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() 得
得![]() 且
且![]()
∴![]() ,
,
易得![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() 且
且![]() ,
,
则![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() .
.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案【题目】某公司为了解用户对其产品的满意度,从A、B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地区: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度的平均值及分散程度(不要求算出具体值,给出结论即可):

(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”,假设两地区用户的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率。
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
【题目】某高校对生源基地学校一年级的数学成绩进行摸底调查,已知其中两个摸底学校分别有![]() 人、
人、![]() 人,现采用分层抽样的方法从两个学校一共抽取了
人,现采用分层抽样的方法从两个学校一共抽取了![]() 名学生的数学成绩,并作出了频数分别统计表如下:(一年级人数为
名学生的数学成绩,并作出了频数分别统计表如下:(一年级人数为![]() 人的学校记为学校一,一年级人数为1000人的学校记为学校二)
人的学校记为学校一,一年级人数为1000人的学校记为学校二)
学校一
分组 |
|
|
|
|
频道 |
|
|
|
|
分组 |
|
|
|
|
频数 |
|
|
|
|
学校二
分组 |
|
|
|
|
频道 |
|
|
|
|
分组 |
|
|
|
|
频数 |
|
|
|
|
(1)计算![]() ,
,![]() 的值.
的值.
(2)若规定考试成绩在![]() 内为优秀,请分别估计两个学校数学成绩的优秀率;
内为优秀,请分别估计两个学校数学成绩的优秀率;
(3)由以上统计数据填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为两个学校的数学成绩有差异.
的把握认为两个学校的数学成绩有差异.
学校一 | 学校二 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
附:
|
|
|
|
|
|
|
|