题目内容
(09年西城区抽样理)(14分)
已知f (x)、g(x)都是定义在R上的函数,如果存在实数m、n使得h (x) = m f(x)+ng(x),那么称h (x)为f (x)、g(x)在R上生成的一个函数.
设f (x)=x2+ax,g(x)=x+b(![]() R),l(x)= 2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
R),l(x)= 2x2+3x-1,h (x)为f (x)、g(x)在R上生成的一个二次函数.
(Ⅰ)设![]() ,若h (x)为偶函数,求
,若h (x)为偶函数,求![]() ;
;
(Ⅱ)设![]() ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
(Ⅲ)试判断h(x)能否为任意的一个二次函数,并证明你的结论.
解析:(Ⅰ)解:设h(x) = m f(x)+ng(x),
则![]() ,
,
因为![]() 为一个二次函数,且为偶函数,
为一个二次函数,且为偶函数,
所以二次函数![]() 的对称轴为y轴,即
的对称轴为y轴,即![]() ,
,
所以![]() ,则
,则![]() ,
,
则![]() ; ------------3分
; ------------3分
(Ⅱ)解:由题意, 设![]() (
(![]() R, 且
R, 且![]() )
)
由h (x)同时也是g(x)、l(x) 在R上生成的一个函数,
知存在![]() 使得
使得![]() ,
,
所以函数![]()
![]() ,
,
则 , ------------5分
, ------------5分
消去![]() , 得
, 得![]() ,
,
因为![]() , 所以
, 所以![]() , ----------7分
, ----------7分
因为b>0,
所以![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
故a+b的最小值为![]() . -----------9分
. -----------9分
(Ⅲ)结论:函数h(x)不能为任意的一个二次函数.
以下给出证明过程.
证明:假设函数h(x)能为任意的一个二次函数,
那么存在m1, n1使得h(x)为二次函数y=x2, 记为![]() ,
,
即![]() ; ①
; ①
同理,存在m2, n2使得h(x)为二次函数![]() ,记为
,记为![]() ,
,
即![]() . ②
. ②
由②-①,得函数![]() ,
,
令![]() ,化简得
,化简得![]() 对
对![]() R恒成立,
R恒成立,
即![]() 对
对![]() R恒成立,
R恒成立,
所以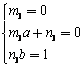 , 即
, 即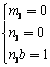 ,
,
显然,![]() 与
与![]() 矛盾,
矛盾,
所以,假设是错误的,
故函数h(x)不能为任意的一个二次函数. ---------14分
注:第(Ⅲ)问还可以举其他反例.
 名校课堂系列答案
名校课堂系列答案