题目内容
已知直线l:y=kx+1(k∈R),圆C:
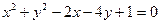 .
.(1)当k=3时,设直线l与圆C交于点A、B,求
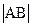 ;
;(2)求证:无论k取何值,直线l恒与圆C相交.
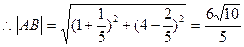
(1)当k=3时,直线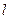 的方程为y=3x+1
的方程为y=3x+1
 y=3x+1
y=3x+1
设A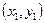 ,B
,B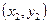 ,由
,由 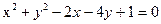
得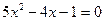 (2分)
(2分)
解得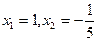 ,带入y=3x+1,得
,带入y=3x+1,得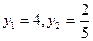 (4分)
(4分)
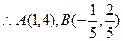 ,
,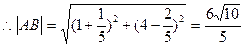 (5分)
(5分)
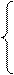 (2)由 y=kx+1
(2)由 y=kx+1
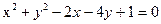
得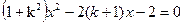 (7分)
(7分)
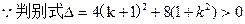 (8分)
(8分)
所以方程组有两个不同的解,所以直线l恒与圆C相交.(10分)
 的方程为y=3x+1
的方程为y=3x+1 y=3x+1
y=3x+1设A
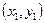 ,B
,B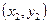 ,由
,由 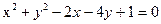
得
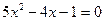 (2分)
(2分)解得
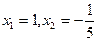 ,带入y=3x+1,得
,带入y=3x+1,得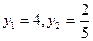 (4分)
(4分)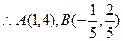 ,
,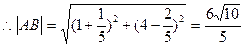 (5分)
(5分) (2)由 y=kx+1
(2)由 y=kx+1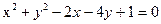
得
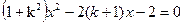 (7分)
(7分)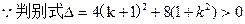 (8分)
(8分)所以方程组有两个不同的解,所以直线l恒与圆C相交.(10分)

练习册系列答案
相关题目
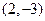 关于直线
关于直线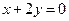 的对称点仍在这个圆上,且圆与
的对称点仍在这个圆上,且圆与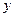 轴相切,求圆的方程。
轴相切,求圆的方程。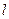 通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线
通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线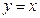 上。
上。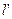 的方程;
的方程;
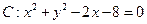 内有一点
内有一点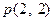 ,过点
,过点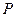 作直线
作直线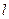 交圆
交圆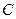 于
于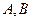 两点.
两点.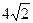 时,求
时,求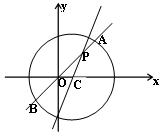
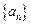 满足:
满足: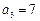 ,
,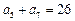 .
.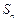 .
.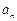 及
及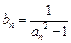 (
(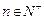 ),求数列
),求数列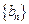 的前n项和
的前n项和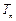 .
. 与圆
与圆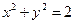 相切,则
相切,则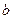 的值为
的值为


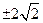
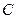 的圆心坐标为
的圆心坐标为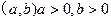 ,若圆
,若圆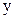 轴相切,在直线
轴相切,在直线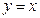 上截得的弦长为
上截得的弦长为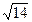 ,且圆心在直线
,且圆心在直线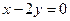 上。
上。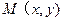 圆
圆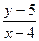 的取值范围。
的取值范围。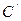 ,若直线
,若直线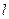 与两坐标轴正半轴的交点分别为
与两坐标轴正半轴的交点分别为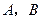 ,直线
,直线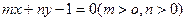 。当
。当
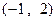 且与圆
且与圆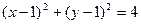 相切的直线方程为
相切的直线方程为 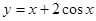 在
在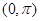 上的单调递减区间为 .
上的单调递减区间为 .