题目内容
设点P(x0,y0)在直线x=m(y![]()
![]() m,0<m<1)上,过点P作双曲线x2-y2=1的两条切线PA、PB,切点为A、B,定点M(
m,0<m<1)上,过点P作双曲线x2-y2=1的两条切线PA、PB,切点为A、B,定点M(![]() ,0).
,0).
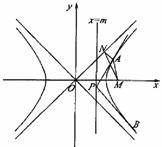
(1)过点A作直线x-y=0的垂线,垂足为N,试求![]() 的重心G所在的曲线方程;
的重心G所在的曲线方程;
(2)求证:A、M、B三点共线.
解:设A(x1,y1),B(x2,y2)由已知得到![]() 且
且![]() ,
,
(1)垂线![]() 的方程为
的方程为![]() 。
。
由![]() 得垂足
得垂足![]() 。
。
设重心![]() ,
,
所以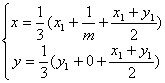 ,解得
,解得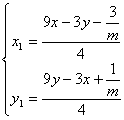
由![]() 可得
可得![]()
即![]() 为重心
为重心![]() 所在曲线方程。
所在曲线方程。
(2)设切线PA的方程为![]()
由![]() 得
得![]()
从而![]() ,解得
,解得![]()
因此PA的方程为![]()
因此PB的方程为![]()
又![]() 在PA、PB上,所以
在PA、PB上,所以![]()
即点![]() 都在直线
都在直线![]() 上
上
又![]() 也在直线
也在直线![]() 上,所以
上,所以![]() 三点共线。
三点共线。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目