题目内容
甲、乙两人独立地破译密码的概率分别为(1)两个人都译出密码的概率;
(2)两个人都译不出密码的概率;
(3)恰有一人译出密码的概率;
(4)至多一人译出密码的概率;
(5)至少一人译出密码的概率.
思路分析:把甲独立破译记为事件A,乙独立破译记为事件B,A与B相互独立, ![]() 与B也相互独立.
与B也相互独立.
解:记A为甲独立的译出密码,B为乙独立的译出?密码.
(1)两个人都译出密码的概率P(AB)=P(A)P(B)=![]() .
.
(2)两个人都译不出密码的概率为P(![]() )=P(
)=P(![]() )P(
)P(![]() )=[1-P(A)][1-P(B)]=
)=[1-P(A)][1-P(B)]=![]() .
.
(3)恰有一人译出密码分为两类:甲译出乙译不出;乙译出甲译不出,即![]()
∴P(![]() )=P(
)=P(![]() )+P(
)+P(![]() )=P(A)P(
)=P(A)P(![]() )+P(
)+P(![]() )P(B)=
)P(B)=![]() .
.
(4)至多一人译出密码的对立事件是两人都译出密码,
∴1-P(AB)=1-P(A)P(B)=![]() .
.
(5)至少一人译出密码的对立事件为两人都没有译出密码,
∴1-P(![]() )=
)=![]() .
.
绿色通道:求相互独立事件同时发生的概率时,运用公式P(AB)=P(A)P(B).在解决问题时,要搞清事件是否独立,同时要注意把复杂事件分解为若干简单事件来处理,同时还要注意运用对立事件把问题简化.

练习册系列答案
相关题目
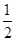 和
和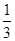 , 求:
, 求: