题目内容
(1)已知函数f(x)=ex-1-tx,?x0∈R,使f(x0)≤0,求实数t的取值范围;
(2)证明: <ln
<ln <
< ,其中0<a<b;
,其中0<a<b;
(3)设[x]表示不超过x的最大整数,证明:[ln(1+n)]≤[1+ + +
+ + ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).
(1)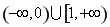 .(2)(3)见解析
.(2)(3)见解析
【解析】
试题分析:(1)根据题意,其实是求实数t的取值范围使函数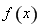 的最小值小于零,结合函数
的最小值小于零,结合函数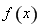 的解析式的特点,应利导数工具,研究函数
的解析式的特点,应利导数工具,研究函数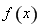 的单调性和极(最)值问题.(2)要证
的单调性和极(最)值问题.(2)要证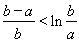 ,即证:
,即证: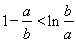 ,只要证:
,只要证: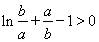 ,因为
,因为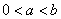 ,所以,
,所以, ,因此可构造函数
,因此可构造函数 ,利用导数探究其在
,利用导数探究其在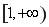 符号即可.类似的方法可证明
符号即可.类似的方法可证明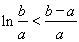 ,必要时可借用(1)的结论.
,必要时可借用(1)的结论.
(3)根据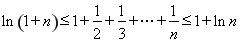
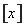 的定义,
的定义,
要证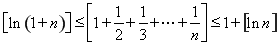
只需证: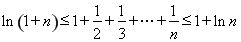
由(2)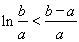 ,若令
,若令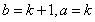 ,则有
,则有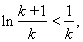
当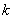 分别取
分别取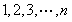 时有:
时有: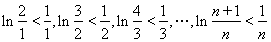
上述同向不等式两边相加可得: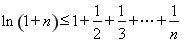 ,类似地可证另一部分.
,类似地可证另一部分.
试题解析:(1)若t<0,令x=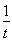 ,则f(
,则f(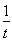 )=e
)=e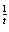 -1-1<0;
-1-1<0;
若t=0,f(x)=ex-1>0,不合题意;
若t>0,只需f(x)min≤0.
求导数,得f′(x)=ex-1-t.
令f′(x)=0,解得x=lnt+1.
当x<lnt+1时,f′(x)<0,∴f(x)在(-∞,lnt+1)上是减函数;
当x>lnt+1时,f′(x)>0,∴f(x)在(lnt+1,+∞)上是增函数.
故f(x)在x=lnt+1处取得最小值f(lnt+1)=t-t(lnt+1)=-tlnt.
∴-tlnt≤0,由t>0,得lnt≥0,∴t≥1.
综上可知,实数t的取值范围为(-∞,0)∪[1,+∞). 4分
(2)由(1),知f(x)≥f(lnt+1),即ex-1-tx≥-tlnt.
取t=1,ex-1-x≥0,即x≤ex-1.
当x>0时,lnx≤x-1,当且仅当x=1时,等号成立,
故当x>0且x≠1时,有lnx<x-1.
令x=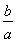 ,得ln
,得ln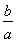 <
<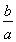 -1(0<a<b),即ln
-1(0<a<b),即ln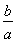 <
<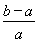 .
.
令x=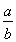 ,得ln
,得ln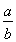 <
<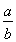 -1(0<a<b),即-ln
-1(0<a<b),即-ln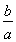 <
<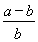 ,亦即ln
,亦即ln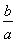 >
>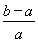 .
.
综上,得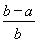 <ln
<ln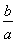 <
<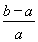 . 9分
. 9分
(3)由(2),得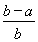 <ln
<ln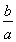 <
<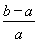 .
.
令a=k,b=k+1(k∈N*),得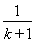 <ln
<ln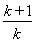 <
<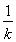 .
.
对于ln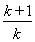 <
<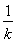 ,分别取k=1,2, ,n,
,分别取k=1,2, ,n,
将上述n个不等式依次相加,得
ln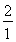 +ln
+ln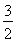 + +ln
+ +ln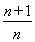 <1+
<1+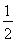 + +
+ +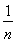 ,
,
∴ln(1+n)<1+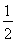 + +
+ +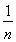 . ①
. ①
对于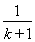 <ln
<ln ,分别取k=1,2, ,n-1,
,分别取k=1,2, ,n-1,
将上述n-1个不等式依次相加,得
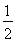 +
+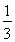 + +
+ + <ln
<ln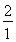 +ln
+ln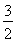 + +ln
+ +ln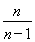 ,即
,即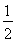 +
+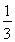 + +
+ +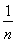 <lnn(n≥2),
<lnn(n≥2),
∴1+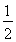 + +
+ +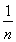 ≤1+lnn(n∈N*). ②
≤1+lnn(n∈N*). ②
综合①②,得ln(1+n)<1+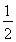 + +
+ + ≤1+lnn.
≤1+lnn.
易知,当p<q时,[p]≤[q],
∴[ln(1+n)]≤[1+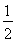 + +
+ +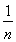 ]≤[1+lnn](n∈N*).
]≤[1+lnn](n∈N*).
又∵[1+lnn]=1+[lnn],
∴[ln(1+n)]≤[1+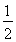 + +
+ +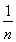 ]≤1+[lnn](n∈N*). 14分
]≤1+[lnn](n∈N*). 14分
考点:1、导数在研究函数性质中的应用;2、对数的运算性质;3、构造函数解决不等式问题.
