题目内容
已知（a-x）5=a0+a1x+a2x2+••+a5x5，若a2=80，则a0+a1+a2+••+a5=
- A.32
- B.1
- C.-243
- D.1或-243
B
分析：利用二项展开式的通项求出通项，令x的指数为2求出a2，列出方程求出a，令二项展开式的x=1求出展开式的系数和．
解答：（a-x）5展开式通项为Tr+1=（-1）ra 5-rC5rxr
令r=2得
a2=a3C52=80，知a=2
令二项展开式的x=1得18=1=a0+a1+…+a8
故选B．
点评：本题考查利用二项展开式的通项公式解决展开式的特定项问题；通过给二项式的x赋值求展开式的系数和．
分析：利用二项展开式的通项求出通项，令x的指数为2求出a2，列出方程求出a，令二项展开式的x=1求出展开式的系数和．
解答：（a-x）5展开式通项为Tr+1=（-1）ra 5-rC5rxr
令r=2得
a2=a3C52=80，知a=2
令二项展开式的x=1得18=1=a0+a1+…+a8
故选B．
点评：本题考查利用二项展开式的通项公式解决展开式的特定项问题；通过给二项式的x赋值求展开式的系数和．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
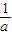+x）4（a∈R，a≠0）的展开式中x的系数为k2，则（ ）
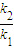为定值