题目内容
函数
 ,
, 的最小值为
的最小值为

 ,
, 的最小值为
的最小值为 4
本试题主要是考查了函数的最值的运用。可以运用导数的思想判定单调性得到。
因为函数
 ,
, ,那么
,那么
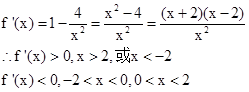
可知在(0,2)递减,在(2,+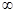 )上递增,因此可知当x=2函数取得极小值f(2)=4,即为最小值为4.故答案为4.
)上递增,因此可知当x=2函数取得极小值f(2)=4,即为最小值为4.故答案为4.
解决该试题的关键是求解导数,判定单调性,易错点就是直接运用均值不等式求解最值,不考虑等号是否能取到。
因为函数

 ,
, ,那么
,那么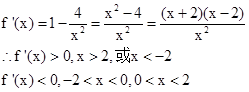
可知在(0,2)递减,在(2,+
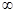 )上递增,因此可知当x=2函数取得极小值f(2)=4,即为最小值为4.故答案为4.
)上递增,因此可知当x=2函数取得极小值f(2)=4,即为最小值为4.故答案为4.解决该试题的关键是求解导数,判定单调性,易错点就是直接运用均值不等式求解最值,不考虑等号是否能取到。

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
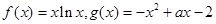 .
.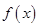 在
在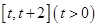 上的最小值;
上的最小值;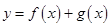 有两个不同的极值点
有两个不同的极值点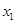 、
、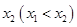 且
且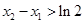 ,求实数
,求实数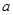 的取值范围.
的取值范围.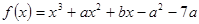 在
在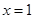 处取得极大值
处取得极大值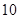 ,则
,则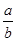 的值为( )
的值为( )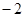
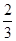
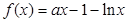
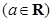 .
.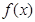 在定义域内的极值点的个数;
在定义域内的极值点的个数;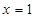 处取得极值,对
处取得极值,对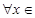
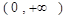 ,
,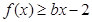 恒成立,求实数
恒成立,求实数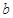 的取值范围.
的取值范围. 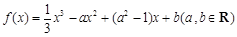
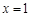 为
为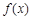 的极值点,求
的极值点,求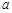 的值;
的值;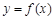 的图象在点
的图象在点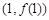 处的切线方程为
处的切线方程为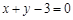 ,求
,求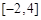 上的最大值;
上的最大值;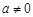 时,若
时,若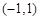 上不单调,求
上不单调,求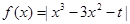
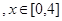 的最大值记为g(t),当t在实数范围内变化时g(t)最小值为
的最大值记为g(t),当t在实数范围内变化时g(t)最小值为 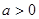 ,函数
,函数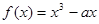 在
在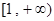 上是单调增函数,则
上是单调增函数,则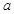 的最大值是
的最大值是