题目内容
直线y=2x+m和圆x2+y2=1交于点A、B，以x轴的正方向为始边，OA为终边（O是坐标原点）的角为α，OB为终边的角为β，若
，那么sin（α-β）的值是______
【答案】分析：△A0B中，由余弦定理可得cos∠A0B=-
，故∠A0B=
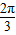，根据α-β=±∠A0B，求得sin（α-β）的值．
解答：解：由题意可得|OA|=|OB|=1，△A0B中，由余弦定理可得 3=1+1-2cos∠A0B，
∴cos∠A0B=-
，∴∠A0B=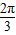
，∴α-β=±
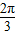，故sin（α-β）=
，
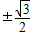故答案为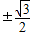
．
点评：本题考查余弦定理的应用，根据三角函数的值求角，得到 α-β=±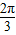
，是解题的关键．
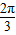，故∠A0B=，根据α-β=±∠A0B，求得sin（α-β）的值．解答：解：由题意可得|OA|=|OB|=1，△A0B中，由余弦定理可得 3=1+1-2cos∠A0B，
∴cos∠A0B=-
，∴∠A0B=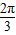，∴α-β=±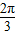，故sin（α-β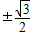）=，故答案为
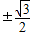．点评：本题考查余弦定理的应用，根据三角函数的值求角，得到 α-β=±
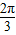，是解题的关键． 
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目