题目内容
设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.,
的左、右焦点.,
(1)若P是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)是否存在过点A(5,0)的直线l与椭圆交于不同的两点C、D,使得|F2C|=|F2D|?若存在,求直线l的方程;若不存在,请说明理由.
解析:(1)易知![]()
设P(x,y),则![]()
![]()
![]() ,
,
![]() ,即点P为椭圆短轴端点时,
,即点P为椭圆短轴端点时,![]() 有最小值3;
有最小值3;
当![]() ,即点P为椭圆长轴端点时,
,即点P为椭圆长轴端点时,![]() 有最大值4
有最大值4
(2)假设存在满足条件的直线l易知点A(5,0)在椭圆的外部,当直线l的斜率不存在时,直线l与椭圆无交点,所在直线l斜率存在,设为k
直线l的方程为![]()
由方程组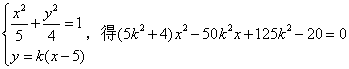
依题意![]()
当![]() 时,设交点C
时,设交点C![]() ,CD的中点为R
,CD的中点为R![]() ,
,
则![]()
![]()
又|F2C|=|F2D|![]()
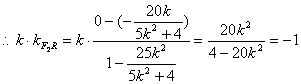
∴20k2=20k2-4,而20k2=20k2-4不成立, 所以不存在直线![]() ,使得|F2C|=|F2D|
,使得|F2C|=|F2D|

练习册系列答案
相关题目
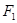 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点. 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求 的最大值和最小值;
的最大值和最小值;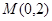 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点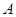 、
、 ,且∠
,且∠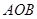 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点. 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
 的取值范围;
的取值范围;  与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠ 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. 是它的两个顶点,直线
是它的两个顶点,直线 与AB相交于点D,与椭圆相交于E、F两点.求四边形
与AB相交于点D,与椭圆相交于E、F两点.求四边形 面积的最大值.
面积的最大值. 、
、 分别是椭圆
分别是椭圆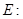
 的左、右焦点,过
的左、右焦点,过 的直线
的直线 与
与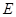 相交于
相交于 、
、 两点,且
两点,且 、
、 、
、 成等差数列.
成等差数列. ,求
,求 ,设点
,设点 满足
满足 ,求椭圆
,求椭圆