题目内容
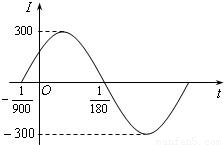
已知交流电的电流强度I（安培）与时间t（秒）满足函数关系式I=f（t）=Asin（ωt+φ），其中A＞0，ω＞0，0≤?＜2π，如图所示的是一个周期内的函数图象．（1）求I=f（t）的解析式；
（2）求y=f（-t）的单调区间．
分析：（1）由函数的最大、最小值，求出振幅A=300．根据函数的周期为T=
，利用周期公式解出ω=150π．最后根据当x=
时函数有最大值300，代入解析式建立关于φ的等式解出φ=-
，即可得到函数I=f（t）的解析式．
（2）由（1）的解析式，可得f（-t）=300sin（-150πt+
）=-300sin（150πt-
），再利用正弦函数单调区间的公式，解关于t的不等式，即可得到所求y=f（-t）的单调区间．
| 1 |
| 75 |
| 1 |
| 450 |
| π |
| 6 |
（2）由（1）的解析式，可得f（-t）=300sin（-150πt+
| π |
| 6 |
| π |
| 6 |
解答：解：（1）∵函数的最大最小值分别为300、-300，且A＞0，∴A=300．
又∵函数的周期T=
-（-
）=
，且ω＞0，
∴
=
，解之得ω=150π．
可得函数的解析式为I=300sin（150πt+φ），
又∵当t=-
+
×
=
时，函数有最大值为300，
∴2sin（150π•
+φ）=300，得sin（
+φ）=1，可得
+φ=
+2kπ（k∈Z）
∵0≤?＜2π，∴取k=0得φ=
-
=
．
∴函数的解析式为I=f（t）=300sin（150πt+
）；
（2）∵I=f（t）=300sin（150πt+
），
∴f（-t）=300sin（-150πt+
）=-300sin（150πt-
），
令-
+2kπ≤150πt-
≤
+2kπ（k∈Z），
解得-
+
≤t≤
+
（k∈Z），
∴y=f（-t）的单调递增区间为[-
+
，
+
]（k∈Z），
同理可得y=f（-t）的单调递减区间为[
+
，
+
，]（k∈Z）．
又∵函数的周期T=
| 11 |
| 900 |
| 1 |
| 900 |
| 1 |
| 75 |
∴
| 2π |
| ω |
| 1 |
| 75 |
可得函数的解析式为I=300sin（150πt+φ），
又∵当t=-
| 1 |
| 900 |
| 1 |
| 4 |
| 1 |
| 75 |
| 1 |
| 450 |
∴2sin（150π•
| 1 |
| 450 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
∵0≤?＜2π，∴取k=0得φ=
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数的解析式为I=f（t）=300sin（150πt+
| π |
| 6 |
（2）∵I=f（t）=300sin（150πt+
| π |
| 6 |
∴f（-t）=300sin（-150πt+
| π |
| 6 |
| π |
| 6 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得-
| 1 |
| 450 |
| k |
| 75 |
| 1 |
| 225 |
| k |
| 75 |
∴y=f（-t）的单调递增区间为[-
| 1 |
| 450 |
| k |
| 75 |
| 1 |
| 225 |
| k |
| 75 |
同理可得y=f（-t）的单调递减区间为[
| 1 |
| 225 |
| k |
| 75 |
| 1 |
| 90 |
| k |
| 75 |
点评：本题以交流电的电流强度I（安培）与时间t（秒）满足的函数关系式为载体，考查了三角函数的图象与性质及其应用的知识，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
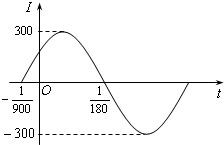已知交流电的电流强度I（安培）与时间t（秒）满足函数关系式I=Asin（ωt+φ），其中A＞0，ω＞0，0≤φ＜2π．
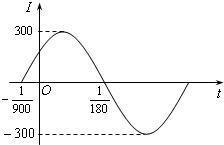已知交流电的电流强度I（安培）与时间t（秒）满足函数关系式I=Asin（ωt+φ），其中A＞0，ω＞0，0≤φ＜2π．
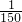秒的时间内电流强度I能同时取得最大值A和最小值-A，那么正整数ω的最小值是多少？
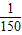秒的时间内电流强度I能同时取得最大值A和最小值-A，那么正整数ω的最小值是多少？