题目内容
【题目】正四棱锥V﹣ABCD中,底面ABCD是边长2为的正方形,其他四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 
(1)求正四棱锥V﹣ABCD的体积.
(2)求二面角V﹣BC﹣A的平面角的大小.
【答案】
(1)解:连结AC,BD,交于点O,连结VO,
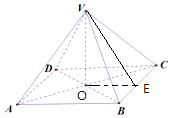
∵正四棱锥V﹣ABCD中,底面ABCD是边长2为的正方形,
其他四个侧面都是侧棱长为 ![]() 的等腰三角形,
的等腰三角形,
∴AO= ![]() =
= ![]() =
= ![]() ,VO=
,VO= ![]() =
= ![]() ,
,
∴正四棱锥V﹣ABCD的高VO= ![]() ,
,
∴正四棱锥V﹣ABCD的体积:
VV﹣ABCD= ![]() =
= ![]() =
= ![]() .
.
(2)解:取BC中点E,连结OE,VE,
则OE⊥BC,VE⊥BC,∴∠VEO是二面角V﹣BC﹣A的平面角,
∵VO= ![]() OE=1,
OE=1,
∴tan ![]() =
= ![]() ,∴∠VEO=60°.
,∴∠VEO=60°.
∴二面角V﹣BC﹣A的平面角的大小为60°.
【解析】(1)连结AC,BD,交于点O,连结VO,求出正四棱锥V﹣ABCD的高VO= ![]() ,由此能求出正四棱锥V﹣ABCD的体积.(2)取BC中点E,连结OE,VE,则OE⊥BC,VE⊥BC,∠VEO是二面角V﹣BC﹣A的平面角,由此能求出二面角V﹣BC﹣A的平面角的大小.
,由此能求出正四棱锥V﹣ABCD的体积.(2)取BC中点E,连结OE,VE,则OE⊥BC,VE⊥BC,∠VEO是二面角V﹣BC﹣A的平面角,由此能求出二面角V﹣BC﹣A的平面角的大小.

练习册系列答案
相关题目