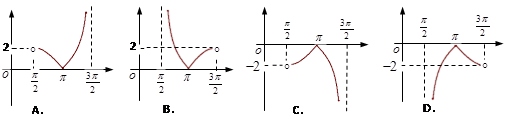题目内容
已知函数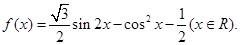
(I)求函数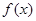 的最小值和最小正周期;
的最小值和最小正周期;
(II)设△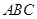 的内角
的内角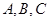 对边分别为
对边分别为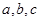 ,且
,且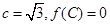 ,若
,若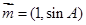 与
与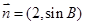 共线,求
共线,求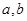 的值.
的值.
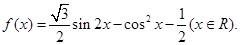
(I)求函数
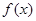 的最小值和最小正周期;
的最小值和最小正周期;(II)设△
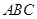 的内角
的内角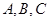 对边分别为
对边分别为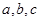 ,且
,且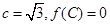 ,若
,若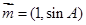 与
与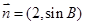 共线,求
共线,求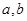 的值.
的值.解:(I)∴函数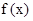 的最小值为-2,当且仅当
的最小值为-2,当且仅当 时取得,最小正周期为
时取得,最小正周期为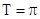 .(II)a=1,b=2.
.(II)a=1,b=2.
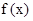 的最小值为-2,当且仅当
的最小值为-2,当且仅当 时取得,最小正周期为
时取得,最小正周期为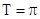 .(II)a=1,b=2.
.(II)a=1,b=2.本试题主要考查了三角函数与解三角形的综合运用。第一问中,利用化为单一三角函数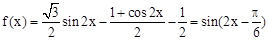 ,得到函数的最值和最小正周期。第二问中,因为
,得到函数的最值和最小正周期。第二问中,因为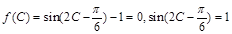 ,得到
,得到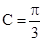 ,然后利用
,然后利用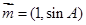 与
与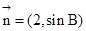 共线共线得到结论。
共线共线得到结论。
解:(I)∵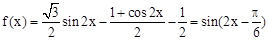 -------2分
-------2分
∴函数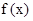 的最小值为-2,当且仅当
的最小值为-2,当且仅当 时取得,最小正周期为
时取得,最小正周期为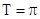 .
.
(II)由题意可知,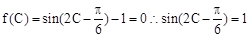 ,
,
∵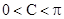 ∴
∴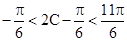 ∴
∴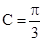 . ----------6分
. ----------6分
∵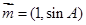 与
与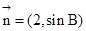 共线∴
共线∴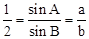 ① ----8分
① ----8分
∵ ② ---10分
② ---10分
由①②解得,a=1,b=2.
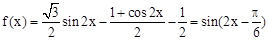 ,得到函数的最值和最小正周期。第二问中,因为
,得到函数的最值和最小正周期。第二问中,因为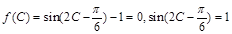 ,得到
,得到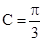 ,然后利用
,然后利用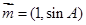 与
与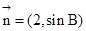 共线共线得到结论。
共线共线得到结论。解:(I)∵
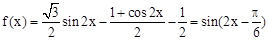 -------2分
-------2分∴函数
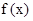 的最小值为-2,当且仅当
的最小值为-2,当且仅当 时取得,最小正周期为
时取得,最小正周期为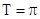 .
.(II)由题意可知,
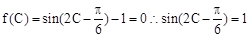 ,
,∵
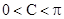 ∴
∴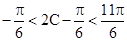 ∴
∴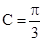 . ----------6分
. ----------6分∵
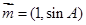 与
与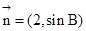 共线∴
共线∴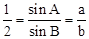 ① ----8分
① ----8分∵
 ② ---10分
② ---10分由①②解得,a=1,b=2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
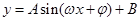 的一部分图像如图所示,如果
的一部分图像如图所示,如果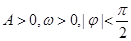 .
.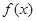 的解析式;
的解析式;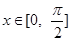 ,求
,求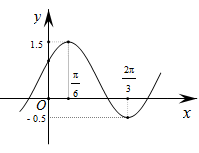
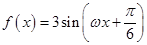 ,
,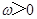 ,
,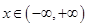 ,且以
,且以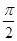 为最小正周期.
为最小正周期.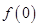 ;
; 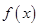 的解析式;
的解析式;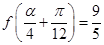 ,
,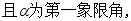 求
求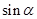 的值.
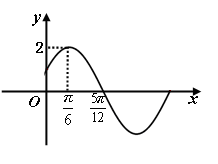
的值.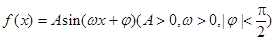 的部分图象如下图所示,则.
的部分图象如下图所示,则. =
=  =
= 
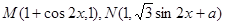
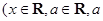 是常数),且
是常数),且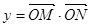 (其中
(其中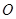 为坐标原点).
为坐标原点).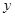 关于
关于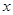 的函数关系式
的函数关系式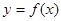 ;
;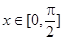 时,
时,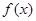 的最大值为4,求
的最大值为4,求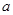 的值.
的值.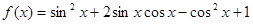
 R
R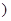 .
.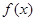 的最大值,并指出此时
的最大值,并指出此时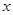 的值.
的值. 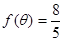 ,求
,求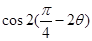 的值.
的值.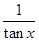 )sin2x-2sin(x+
)sin2x-2sin(x+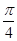 )sin(x-
)sin(x- ,
,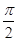 ],求f(x)的取值范围
],求f(x)的取值范围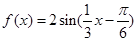 ,
,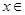
 .(13分)
.(13分)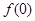 的值;
的值; ,
,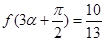 ,
,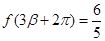 ,求
,求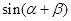 的值.
的值.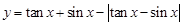 在区间
在区间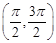 内的图象是( )
内的图象是( )