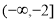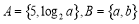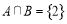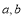题目内容
设函数
满足
且
．
（1）求证
，并求
的取值范围；
（2）证明函数
在
内至少有一个零点；
（3）设
是函数
的两个零点，求
的取值范围．
（1）详见解析，（2）详见解析，（3）
.
【解析】
试题分析：（1）由等量关系消去C是解题思路，揭示a为正数是解题关键，本题是典型题，实质是三个实数和为零，则最大的数必为正数，最小的数必为负数，中间的数不确定，通常被消去，（2）证明区间内有解首选零点存在定理.连续性不是高中数学考核的知识点，重点考核的是区间端点函数值的符号.要确定区间端点函数值的符号，需恰当选择区间端点，这是应用零点存在定理的难点，本题
符号确定，但
符号不确定．由于两者符号与
有关，所以需要对进行讨论，（3）要求
的取值范围，需先运用韦达定理建立函数解析式（二次函数），再利用（1）的范围（定义域），求二次函数值域.本题思路简单，但不能忽视定义域在解题中作用.
试题解析：（1）由题意得
，
又
，
2分
由
，得
，
，得
5分
（2）
，
又
，
若
则
，
在
上有零点；
若
则
，
在
上有零点
函数
在
内至少有一个零点 9分
（3）
， 13分
考点：二次函数值域，零点存在定理.
练习册系列答案
相关题目
