题目内容
使关于x的不等式|x+1|+k＜x有解的实数k的取值范围是（ ）
| A、（-∞，-1） | B、（-∞，1） | C、（-1，+∞） | D、（1，+∞） |
分析：把原不等式先转化为k＜x-|x+1|成立，再借助于图象求出x-|x+1|的最大值，即可求出实数k的取值范围．
解答：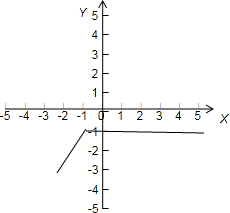
解：原不等式转化为k＜x-|x+1|成立，
因为y=x-|x+1|=
对应图象如图，
由图得其最大值为-1．
故只须k＜-1即可．
故选A．
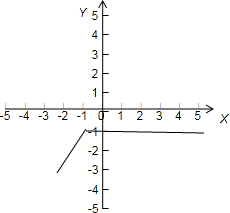解：原不等式转化为k＜x-|x+1|成立，因为y=x-|x+1|=
|
由图得其最大值为-1．
故只须k＜-1即可．
故选A．
点评：本题考查带绝对值不等式的应用问题．在解带绝对值的不等式时，一般先去绝对值符号，再分别求解，最后综合即可．
练习册系列答案
阅读快车系列答案
相关题目