题目内容
若a>0,使关于x的不等式|x-3|+|x-4|<a在R上的解集不是空集,设a的取值集合是A;若不等式|x|>bx(b∈R)的解集为(0,+∞),设实数b的取值集合是B,试求当x∈A∪B时,f(x)=2|x+1|-|x-1|的值域.
【答案】分析:利用不等式的性质对|x-3|+|x-4|进行放缩和分类讨论,求出|x-3|-|x-4|的最小值,即可求a的取值集合,根据不等式|x|>bx,分两种情况进行讨论,根据其解集为(0,+∞),求出b的范围,根据交集运算法则,求出A∪B,去掉绝对值求出f(x)的值域;
解答:解:|x-3|+|x-4|的几何意义是数轴上的点x 到3和4的距离之和,
当x在3、4之间时,这个距离和最小为是1,其它情况都大于1
所以|x-3|+|x-4|≥1
如果使关于x的不等式|x-3|+|x-4|<a在R上的解集不是空集,所以 a>1,
∴A={a|a>1};
不等式|x|>bx(b∈R)的解集为(0,+∞),
当x>0时,x-bx>0,即x(1-b)>0,∴1-b>0,∴b<1;
当x<0时,-x-bx>0,即x(1+b)<0,∴1+b>0,∴b>-1,
∵不等式|x|>bx(b∈R)的解集为(0,+∞),说明x<0时x无解,得b≤-1,
综上:b<-1;B={b|b≤-1}
∴A∪B={a|a>1}∪{b|b≤-1};
∵f(x)=2|x+1|-|x-1|,
当x>1时,f(x)=2x+1-x+1,f(x)为单调增函数,f(x)>f(1)=4;
当x≤-1时,f(x)=2-x-1+x-1,f′(x)=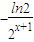 +1<0,f(x)为减函数,f(x)≥f(-1)=-1;
+1<0,f(x)为减函数,f(x)≥f(-1)=-1;
∴综上:当x>1时,f(x)>4;当x<-1时,f(x)≥-1;
点评:此题考查绝对值不等式的求解问题及函数的恒成立问题,这类题目是高考的热点,难度不是很大,考查分段函数的性质,此题考查的知识点比较多,是一道难题;
解答:解:|x-3|+|x-4|的几何意义是数轴上的点x 到3和4的距离之和,
当x在3、4之间时,这个距离和最小为是1,其它情况都大于1
所以|x-3|+|x-4|≥1
如果使关于x的不等式|x-3|+|x-4|<a在R上的解集不是空集,所以 a>1,
∴A={a|a>1};
不等式|x|>bx(b∈R)的解集为(0,+∞),
当x>0时,x-bx>0,即x(1-b)>0,∴1-b>0,∴b<1;
当x<0时,-x-bx>0,即x(1+b)<0,∴1+b>0,∴b>-1,
∵不等式|x|>bx(b∈R)的解集为(0,+∞),说明x<0时x无解,得b≤-1,
综上:b<-1;B={b|b≤-1}
∴A∪B={a|a>1}∪{b|b≤-1};
∵f(x)=2|x+1|-|x-1|,
当x>1时,f(x)=2x+1-x+1,f(x)为单调增函数,f(x)>f(1)=4;
当x≤-1时,f(x)=2-x-1+x-1,f′(x)=
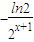 +1<0,f(x)为减函数,f(x)≥f(-1)=-1;
+1<0,f(x)为减函数,f(x)≥f(-1)=-1;∴综上:当x>1时,f(x)>4;当x<-1时,f(x)≥-1;
点评:此题考查绝对值不等式的求解问题及函数的恒成立问题,这类题目是高考的热点,难度不是很大,考查分段函数的性质,此题考查的知识点比较多,是一道难题;

练习册系列答案
相关题目
 ,求函数g(x)解析式;
,求函数g(x)解析式; x0∈(0,+∞),使关于x的不等式2f(x)≥g'(x)+2成立,求实数a取值范围.
x0∈(0,+∞),使关于x的不等式2f(x)≥g'(x)+2成立,求实数a取值范围.