题目内容
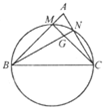 如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若| BM |
| BC |
| CN |
| BC |
分析:由条件求得故M在BC的中垂线上,且∠CBM=45°=∠BCM,N在BC上的投影(设为D)到C的距离为
,利用勾股定理求得ND,可得tan∠CBN的值,从而求得∠CBN 的值.再利用三角形的内角和公式求得∠BGC的值.
| 1 |
| 2 |
解答:解:∵
•
=2,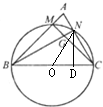
∴BM•BCcos∠CBM=2即BM•cos∠CBM=1,故M在BC的中垂线上,
∴∠CBM=45°=∠BCM,
∵
•
=1,
∴CN•cos(180°-∠NCB)=-
,
∴N在BC上的投影(设为D)到C的距离为
,
设圆心为O,连接ON,
∴CD=OD=
,则 OD2+ND2=ON2=1,解得 ND=
,
∴tan∠CBN=
=
=
,
∴∠CBN=30°,
∴∠BGC=180°-∠CBN-∠BCM=180°-30°-45°=105°,
故选D.
| BM |
| BC |

∴BM•BCcos∠CBM=2即BM•cos∠CBM=1,故M在BC的中垂线上,
∴∠CBM=45°=∠BCM,
∵
| CN |
| BC |
∴CN•cos(180°-∠NCB)=-
| 1 |
| 2 |
∴N在BC上的投影(设为D)到C的距离为
| 1 |
| 2 |
设圆心为O,连接ON,
∴CD=OD=
| 1 |
| 2 |
| ||
| 2 |
∴tan∠CBN=
| ND |
| BD |
| ||||
1+
|
| ||
| 3 |
∴∠CBN=30°,
∴∠BGC=180°-∠CBN-∠BCM=180°-30°-45°=105°,
故选D.
点评:本题主要考查两个向量的数量积的定义,直角三角形中的边角关系,三角形的内角和公式,同时考查了分析问题的能力,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,AC=6,DB=5,则AD的长为( )
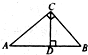

| A、3 | B、4 | C、5 | D、6 |
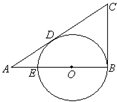
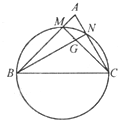 (2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
(2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若