题目内容

（选修4-1：几何证明选讲）如图，已知在△ABC中，∠B=90°．O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，AD=2，AE=1，则CD的长为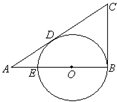
3
3
．
分析：利用圆的切线性质、切割线定理、勾股定理即可得出．
解答：解：由AD与圆O相切于点D，根据切割线定理可得AD2=AE•AB，又AD=2，AE=1，∴AB=
AD2
AE
=4．
由CD，CB都是圆O的切线，根据切线长定理可得，设CD=x，则CB=x．
由切线的性质可得：AB⊥BC，
∴AB2+BC2=AC2，∴42+x2=（x+2）2，得x=3，即CD=3．
故答案为3．
点评：熟练掌握圆的切线性质、切割线定理、勾股定理是解题的关键．
练习册系列答案
相关题目
选修4-1：几何证明选讲
已知⊙O的弦AB长为4，将线段AB延长到点P，使BP=2；过点P作直线PC切⊙O于点C；
（1）求线段PC的长；
（2）作⊙O的弦CD交AB于点Q（CQ＜DQ），且Q为AB中点，又CD=5，求线段CQ的长．
（2013•海口二模）选修4-1：几何证明选讲
切线AB与圆切于点B，圆内有一点C满足AB=AC，∠CAB的平分线AE交圆于D，E，延长EC交圆于F，延长DC交圆于G，连接FG．
（Ⅰ）证明：AC∥FG；
（Ⅱ）求证：EC=EG．
（2012•徐州模拟）本题包括A、B、C、D四小题，请选定其中两题，并在答题卡指定区域内作答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，半径分别为R，r（R＞r＞0）的两圆⊙O，⊙O1内切于点T，P是外圆⊙O上任意一点，连PT交⊙O1于点M，PN与内圆⊙O1相切，切点为N．求证：PN：PM为定值．
B．选修4-2：矩阵与变换
已知矩阵M=
21
34

（1）求矩阵M的逆矩阵；
（2）求矩阵M的特征值及特征向量；
C．选修4-2：矩阵与变换
在平面直角坐标系x0y中，求圆C的参数方程为
x=-1+rcosθ
y=rsinθ
(θ为参数r＞0），以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos(θ+
π
4
)=2
2
．若直线l与圆C相切，求r的值．
D．选修4-5：不等式选讲
已知实数a，b，c满足a＞b＞c，且a+b+c=1，a2+b2+c2=1，求证：1＜a+b＜
4
3
．
选修4-1：几何证明选讲
如图，已知PA与⊙O相切于点A，PBC为⊙O的割线，弦CD∥AP，AD与BC相交于点E，F为CE上一点，且DE2=EF•EC
（I）求证：A、P、D、F四点共圆
（II）若AE=6，DE=EB=4，求PA的长．
（2013•南通一模）选修4-1：几何证明选讲
如图，△ABC是⊙O的内接三角形，若AD是△ABC的高，AE是⊙O的直径，F是
BC
的中点．求证：
（1）AB•AC=AE•AD；
（2）∠FAE=∠FAD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网