题目内容
.(本小题满分12分)
已知数列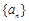 满足:
满足: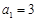 ,
,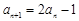 ,
, .计算得
.计算得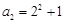 ,
,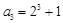 .
.
(1)猜想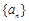 的通项公式
的通项公式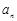 ,并用数学归纳法加以证明;
,并用数学归纳法加以证明;
(2)用反证法证明数列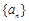 中不存在成等差数列的三项.
中不存在成等差数列的三项.
【答案】
解:(I)猜想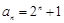 ,
…………2分
,
…………2分
证明如下:
①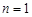 时,
时,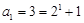 ,等式成立;
,等式成立;
②假设当 时等式成立,即
时等式成立,即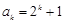 ,
,
那么当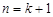 时,
时,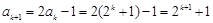 ,
,
所以当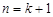 时等式也成立,
时等式也成立,
由①②可知,等式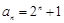 对
对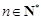 成立; …………6分
成立; …………6分
(II)假设数列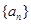 中存在成等差数列的三项
中存在成等差数列的三项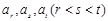 ,则
,则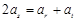 ,….8分
,….8分
∵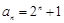 ,∴
,∴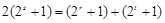 ,即
,即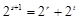
∴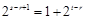 ,
, 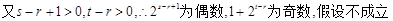
因此,数列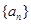 中不存在成等差数列的三项.
…………12分
中不存在成等差数列的三项.
…………12分
【解析】略

练习册系列答案
相关题目