题目内容
直线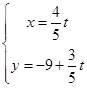
（
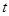为参数）与圆
(
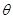为参数)的位置关系是( )
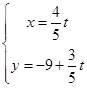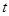（为参数）与圆(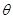为参数)的位置关系是( )| A．相离 | B．相切 | C．过圆心 | D．相交不过圆心 |
A
将直线与圆的参数方程转化为普通方程，利用圆心O（0，0）到直线3x-4y-36=0的距离d=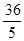
与该圆的半径2比较即可得到答案．
解：将直线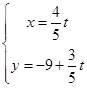（t为参数）消掉参数t转化为普通方程为：3x-4y-36=0，
圆（θ为参数）的普通方程为：(
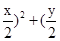)2=cos2θ+sin2θ=1，即x2+y2=4；
∵圆心O（0，0）到直线3x-4y-36=0的距离d=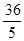＞2，
故该直线与圆x2+y2=4相离．
故选A．
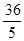与该圆的半径2比较即可得到答案．解：将直线
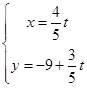（t为参数）消掉参数t转化为普通方程为：3x-4y-36=0，圆
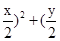（θ为参数）的普通方程为：()2=cos2θ+sin2θ=1，即x2+y2=4；∵圆心O（0，0）到直线3x-4y-36=0的距离d=
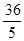＞2，故该直线与圆x2+y2=4相离．
故选A．
练习册系列答案
名校课堂系列答案
相关题目
轴的正半轴重合，曲线C1 
（t为参数），曲线
．
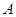，P为OA中点，当
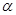变化时，求P点的轨迹的参数方程，并指出它是什么曲线．
中，直线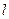
的参数方程为
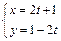（参数t∈R），椭圆C的参数方程为
（
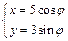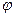为参数），则椭圆C的左焦
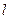的参数方程为
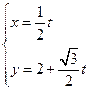（t为参数），曲线C的极坐标方程是
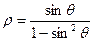以极点为原点，极轴为x轴正方向建立直角坐标系，点
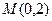，直线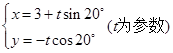
的倾斜角是（ ）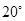
(
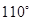
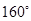
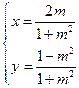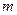是参数)表示的曲线的普通方程是_____________
（
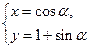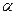为参数）化成普通方程为________________.
,若多做,则按A题记分）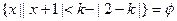
，则实数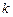
的取值范围是 ；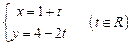
与圆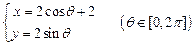
相交于AB,则以AB为直径的圆的面积为 .
（
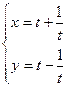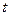为参数）的曲线的焦距为 ．