题目内容
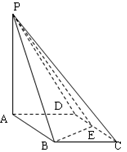
如图,正方形 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△ 是等腰直角三角形,
是等腰直角三角形,

(1)线段 的中点为
的中点为 ,线段
,线段 的中点为
的中点为 ,求证:
,求证: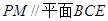 ;
;
(2)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△ 是等腰直角三角形,
是等腰直角三角形,

(1)线段
 的中点为
的中点为 ,线段
,线段 的中点为
的中点为 ,求证:
,求证: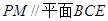 ;
;(2)求直线
 与平面
与平面 所成角的正切值.
所成角的正切值.(1)根据面面平行的性质定理, 面
面 //面
//面 ,可知结论。(2)
,可知结论。(2)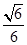
 面
面 //面
//面 ,可知结论。(2)
,可知结论。(2)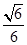
试题分析:(1)取
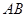 的中点为
的中点为 ,连
,连 ,
, ,则
,则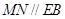 ,
,
 面
面 //面
//面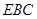 ,
,
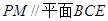 ………………………5分
………………………5分(2)先证出
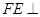 面
面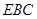 , ………………………8分
, ………………………8分 为直线
为直线 与平面
与平面 所成角, ………………………11分
所成角, ………………………11分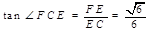 ………………………14分
………………………14分点评:对于平行的证明,主要是根据线面位置关系中平行的判定定理来得到,那么对于线面角的求解,关键是作出平面的垂线来证明,考查了分析问题的能力。中档题。

练习册系列答案
相关题目
 中,
中, 分别是
分别是 ,
,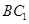 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )
 与
与 垂直
垂直 垂直
垂直 异面
异面 异面
异面 的底面为菱形,且
的底面为菱形,且 ,
,
 ,
, 为
为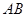 的中点.
的中点.

 平面
平面 ;
; 到面
到面 的距离.
的距离. 是两条不同的直线,
是两条不同的直线, 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: ,则
,则 ②若
②若 则
则 ;
;  则
则 ; ④若
; ④若 则
则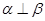 ;
;  中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且 ,
, 为
为 中点.
中点.
 平面
平面 的余弦值.
的余弦值.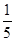 B.
B. 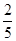 C.
C. 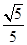 D.
D. 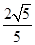
 中,底面
中,底面 是正方形.已知
是正方形.已知 ,
, .
.
 ;
; .
. α,n
α,n BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.