题目内容
18.若函数f(x)=${C}_{n}^{0}$xn+${C}_{n}^{1}{x}^{n-2}$+${C}_{n}^{2}{x}^{n-4}$+…+${C}_{n}^{r}{x}^{n-2r}$+…+${C}_{n}^{n}(\frac{1}{x})^{n}$,其中n∈Nn,则f′(1)=0.分析 求出通项公式的导数,利用组合数的性质,求解导函数值即可.
解答 解:$({C}_{n}^{r}{x}^{n-2r})′$=(n-2r)${C}_{n}^{r}{x}^{n-2r-1}$,
x=1时,上式=(n-2r)${C}_{n}^{r}$,
函数f(x)=${C}_{n}^{0}$xn+${C}_{n}^{1}{x}^{n-2}$+${C}_{n}^{2}{x}^{n-4}$+…+${C}_{n}^{r}{x}^{n-2r}$+…+${C}_{n}^{n}(\frac{1}{x})^{n}$,其中n∈N+,
f′(x)=n${C}_{n}^{0}$xn-1+(n-2)${C}_{n}^{1}$xn-3+(n-4)${C}_{n}^{2}$xn-5+…+(n-2r)${C}_{n}^{r}$xn-2t-1+…+(-n)${C}_{n}^{n}$x-n-1.
则f′(1)=n${C}_{n}^{0}$+(n-2)${C}_{n}^{1}$+(n-4)${C}_{n}^{2}$+…+(n-2r)${C}_{n}^{r}$+…+(-n+2)${C}_{n}^{n-1}$+(-n)${C}_{n}^{n}$.
∵${C}_{n}^{0}={C}_{n}^{n}$,${C}_{n}^{1}={C}_{n}^{n-1}$,…
∴f′(1)=0.
故答案为:0.
点评 本题考查组合数的性质的应用,导数的应用,考查计算能力.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
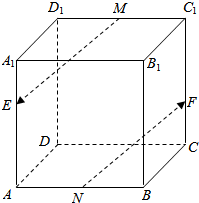 如图,在平行六面体ABCD-A1B1C1D1中,M,N分别是C1D1,AB的中点,E在AA1上且AE=2EA1,F在CC1上且CF=$\frac{1}{2}$FC1,判断$\overrightarrow{ME}$与$\overrightarrow{NF}$是否共线?
如图,在平行六面体ABCD-A1B1C1D1中,M,N分别是C1D1,AB的中点,E在AA1上且AE=2EA1,F在CC1上且CF=$\frac{1}{2}$FC1,判断$\overrightarrow{ME}$与$\overrightarrow{NF}$是否共线?