题目内容
有6名乒乓球运动员分别来自3个不同国家，每一个国家2人，他们排成一排，列队上场，要求同一国家的人不能相邻，那么不同的排法有
- A.720种
- B.432种
- C.360种
- D.240种
D
分析：先排一个国家的两个运动员，有
=2种方法，再用插空法排第二个国家的两个运动员，有
=6种方法，同样的，用插空法排列第三个国家的两名队员，有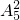
=20种方法，根据
分布计数原理求得结果．
解答：先排一个国家的两个运动员，有=2种方法．
这两个人之间和两端共三个空，再插入第二个国家的两个运动员，有=6种方法．
同样的，排列第三个国家的两名队员，有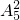=20种方法．
根据分步计数原理，不同的排法共有2×6×20=240种，
故选D．
点评：本题主要考查排列与组合及分布计数原理的应用，属于中档题．
分析：先排一个国家的两个运动员，有
=2种方法，再用插空法排第二个国家的两个运动员，有=6种方法，同样的，用插空法排列第三个国家的两名队员，有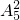=20种方法，根据分布计数原理求得结果．
解答：先排一个国家的两个运动员，有
=2种方法．这两个人之间和两端共三个空，再插入第二个国家的两个运动员，有
=6种方法．同样的，排列第三个国家的两名队员，有
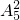=20种方法．根据分步计数原理，不同的排法共有2×6×20=240种，
故选D．
点评：本题主要考查排列与组合及分布计数原理的应用，属于中档题．
练习册系列答案
相关题目
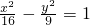的焦点是F1，F2，点P是双曲线上一点，若
=0，则△PF1F2的面积是
已知如图所示的程序框图（未完成），设当箭头a指向①时，输出的结果为S=m，当箭头a指向②时，输出的结果为S=n，则m+n的值为________．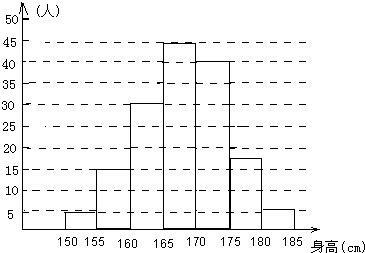
抽取某校学生的一个容量为150的样本，测得学生身高后，得到身高频数分布直方图如图所示，已知该校有学生1500名，则可以估计出该校身高位于160cm至165cm之间大约有______人．