题目内容
【题目】求下列不等式的解集:
(1)![]()
(2)![]()
(3)![]()
(4)![]()
【答案】(1)![]() ;(2)
;(2)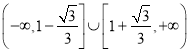 ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)根据一元二次不等式的解法,求得不等式的解集.
(2)根据一元二次不等式的解法,求得不等式的解集.
(3)根据一元二次不等式的解法,求得不等式的解集.
(4)根据一元二次不等式的解法,求得不等式的解集.
(1)方法一(因式分解法)因为![]() ,
,
所以原不等式可化为![]() ,解得
,解得![]() ,
,
所以原不等式的解集为![]() .
.
方法二(配方法)原不等式化为![]() ,因为
,因为![]() ,
,
所以原不等式可化为![]() ,即
,即![]() ,
,
两边开平方,得![]() ,即
,即![]() ,所以
,所以![]() .
.
所以原不等式的解集为![]() .
.
(2)原不等式化为![]() ,因为
,因为![]() ,
,
所以原不等式可化为![]() ,即
,即![]() .两边开平方,得
.两边开平方,得![]() ,
,
即![]() 或
或![]() .所以
.所以![]() 或
或![]() ,
,
所以原不等式的解集为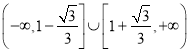 .
.
(3)原不等式可化为![]() ,所以原不等式的解集为
,所以原不等式的解集为![]() .
.
(4)原不等式可化为![]() ,即
,即![]() ,即
,即![]() ,所以原不等式的解集为
,所以原不等式的解集为![]() .
.

 津桥教育计算小状元系列答案
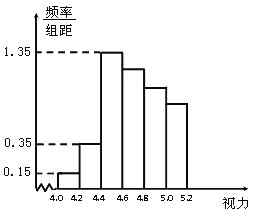
津桥教育计算小状元系列答案【题目】对某电子元件进行寿命追踪调查,情况如下:
寿命分组/h | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个数 | 20 | 30 | 80 | 40 | 30 |
(1)求下表中的x,y;
寿命分组/h | 频数 | 频率 |
100~200 | 20 | 0.10 |
200~300 | 30 | x |
300~400 | 80 | 0.40 |
400~500 | 40 | 0.20 |
500~600 | 30 | y |
合计 | 200 | 1 |
(2)从频率分布直方图估计电子元件寿命的第80百分位数是多少.
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁![]() 59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列2×2列联表,并回答能否有90%的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2 人能胜任的2人能胜任才艺表演的概率是多少?