题目内容
函数的定义域为R,且满足f(x)是偶函数,f(x-1)是奇函数,若f(
)=9,则f(
)=( )
| 1 |
| 2 |
| 25 |
| 2 |
分析:由f(x-1)是奇函数,得到f(-x)=-f(x-2),又f(x)是偶函数,f(x)=f(-x)=-f(x-2),由此可得结论.
解答:解:∵f(x-1)是奇函数,∴f(-x-1)=-f(x-1),∴f(-x)=-f(x-2),
又∵f(x)是偶函数,∴f(x)=f(-x),
∴f(x)=-f(x-2),∴f(x+4)=f(x)
∴f(12.5)=f(3×4+0.5)=f(0.5)=9.
故选B.
又∵f(x)是偶函数,∴f(x)=f(-x),
∴f(x)=-f(x-2),∴f(x+4)=f(x)
∴f(12.5)=f(3×4+0.5)=f(0.5)=9.
故选B.
点评:本题考查函数奇偶性,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 的定义域为R,且定义如下:
的定义域为R,且定义如下: (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足 ,则函数
,则函数 的值域为 ( )
的值域为 ( ) B.
B. C.
C. D.
D.
 的定义域为R,且定义如下:
的定义域为R,且定义如下: (其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足
(其中M是实数集R的非空真子集),在实数集R上有两个非空真子集A、B满足 ,则函数
,则函数 的值域为 ( )
的值域为 ( ) B.
B. C.
C. D.
D.
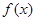 的定义域为R,且
的定义域为R,且

 的取值范围是 ( )
的取值范围是 ( )  B.(
B.(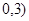 C.(
C.( D.
D.