题目内容

解不等式log3（x2-6x+8 ）-log3x＜1．
分析：由不等式 log3（x2-6x+8 ）-log3x＜1可知由
x＞0
x2-6x+8＞0
，解这个不等式就可以得到原不等式的解集．
解答：解：由
x＞0
x2-6x+8＞0
，得0＜x＜2或x＞4．（4分）
不等式化成：log3（x2-6x+8）＜log33x（4分）
得x2-9x+8＜0．
即（x-8）（x-1）＜0，
解得1＜x＜8时，（4分）
综上得不等式的解为1＜x＜2或4＜x＜8．（2分）
点评：这道题相对比较简单，主要方法就是利用对数函数的性质能把对数不等式转化为一元二次不等式组．
练习册系列答案
相关题目
已知函数g（x）=（a+1）x-2+1（a＞0）的图象恒过定点A，且点A又在函数f(x)=log
3
(x+a)的图象上．
（1）求实数a的值
（2）解不等式g（x）＞3．
已知函数g（x）=（a+1）x-2+1（a＞0）的图象恒过定点A，且点A又在函数f(x)=log
3
(x+a)的图象．
（1）求实数a的值；
（2）解不等式f（x）＜log 
3
a；
（3）|g（x+2）-2|=2b有两个不等实根时，求b的取值范围．
不等式log3（x-1）＞0的解集为
（2，+∞）
（2，+∞）
．
（A类）已知函数g（x）=（a+1）x-2+1（a＞0）的图象恒过定点A，且点A又在函数f（x）=log
3
（x+a）的图象上．
（1）求实数a的值；                （2）解不等式f（x）＜log
3
a；
（3）|g（x+2）-2|=2b有两个不等实根时，求b的取值范围．
（B类）设f（x）是定义在R上的函数，对任意x，y∈R，恒有f（x+y）=f（x）+f（y）
（1）求f（0）的值；     （2）求证：f（x）为奇函数；
（3）若函数f（x）是R上的增函数，已知f（1）=1，且f（2a）＞f（a-1）+2，求a的取值范围．
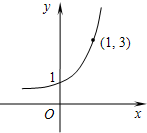（2007•闵行区一模）（文）已知函数f（x）=ax的图象过点P（1，3），解不等式log3（3-x）-logax＜0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网