题目内容
已知函数f(x)满足f(x)=x3+f′(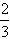 )x2-x+C [其中f′(
)x2-x+C [其中f′(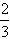 )为f(x)在点x=
)为f(x)在点x=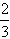 处的导数,C为常数]。
处的导数,C为常数]。
(1)求f′(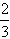 )的值;
)的值;
(2)求函数f(x)的单调区间;
(3)设函数g(x)=[f(x)-x3]ex,若函数g(x)在x∈[-3,2]上单调,求实数C的取值范围。
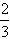 )x2-x+C [其中f′(
)x2-x+C [其中f′(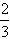 )为f(x)在点x=
)为f(x)在点x=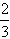 处的导数,C为常数]。
处的导数,C为常数]。(1)求f′(
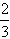 )的值;
)的值;(2)求函数f(x)的单调区间;
(3)设函数g(x)=[f(x)-x3]ex,若函数g(x)在x∈[-3,2]上单调,求实数C的取值范围。
解:(1)由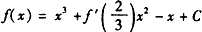 得
得
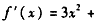
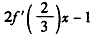
取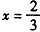 得
得
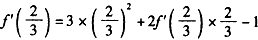
解之得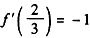 。
。
(2)因为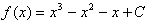
从而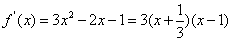
列表如下:
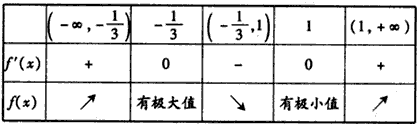
∴f(x)的单调递增区间是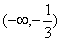 和(1,+∞),
和(1,+∞),
f(x)的单调递减区间是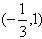 .
.
(3)函数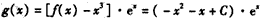
有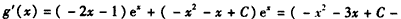
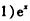
当函数在区间x∈[-3,2]上单调递增时,等价于h(x)= -x2-3x+C-1≥0在x∈[-3,2]上恒成立,
只要h(2)≥0,解得 C≥11
当函数在区间x∈[ -3,2]上单调递减时,等价于h(x)= -x2-3x+C-1≤0在x∈[-3,2]上恒成立,
即Δ=9+4(C-1)≤ 0,解得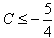
所以C的取值范围是C≥11或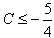 。
。
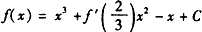 得
得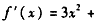
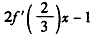
取
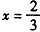 得
得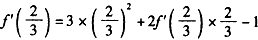
解之得
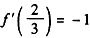 。
。(2)因为
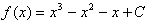
从而
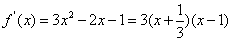
列表如下:

∴f(x)的单调递增区间是
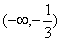 和(1,+∞),
和(1,+∞),f(x)的单调递减区间是
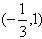 .
.(3)函数
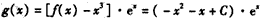
有
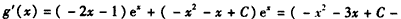
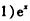
当函数在区间x∈[-3,2]上单调递增时,等价于h(x)= -x2-3x+C-1≥0在x∈[-3,2]上恒成立,
只要h(2)≥0,解得 C≥11
当函数在区间x∈[ -3,2]上单调递减时,等价于h(x)= -x2-3x+C-1≤0在x∈[-3,2]上恒成立,
即Δ=9+4(C-1)≤ 0,解得
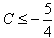
所以C的取值范围是C≥11或
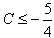 。
。
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目