题目内容
1、有以下命题:
(1)若函数f(x),g(x)在R上是增函数,则f(x)+g(x)在R上也是增函数;
(2)若f(x)在R上是增函数,g(x)在R上是减函数,则g(x)-f(x)在R上是减函数;
(3)若函数f(x)在区间[a,b]上递增,在(b,c)上也递增,则f(x)在[a,c)上递增;
(4)若奇函数f(x)在(0,+∞)上递减,则f(x)在(-∞,0)上也递减.
其中正确命题的个数为
(1)若函数f(x),g(x)在R上是增函数,则f(x)+g(x)在R上也是增函数;
(2)若f(x)在R上是增函数,g(x)在R上是减函数,则g(x)-f(x)在R上是减函数;
(3)若函数f(x)在区间[a,b]上递增,在(b,c)上也递增,则f(x)在[a,c)上递增;
(4)若奇函数f(x)在(0,+∞)上递减,则f(x)在(-∞,0)上也递减.
其中正确命题的个数为
3
个.分析:本题考查的是函数单调性的判断和证明问题,在解答时应注意进行单调性的分析.如:(1)(3)(4)可以通过定义理解,(3)可以通过数形结合画反例解决.
解答:解:(1)若函数f(x),g(x)在R上是增函数,则由函数单调性的定义易知:则f(x)+g(x)在R上也是增函数;
(2)若f(x)在R上是增函数,g(x)在R上是减函数,则函数-f(x)在R上是减函数函数,结合(1)知:g(x)-f(x)在R上是减函数;
(4)若奇函数f(x)在(0,+∞)上递减,由于奇函数关于原点对称,所以f(x)在(-∞,0)上也递减.
而(3)若函数f(x)在区间[a,b]上递增,在(b,c)上也递增,如图:
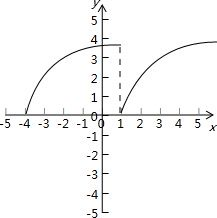
可知函数在[-1,1]是增函数,在(1,2)上也是增函数,但不能说函数在[-1,2)为增函数.
故答案为:3.
(2)若f(x)在R上是增函数,g(x)在R上是减函数,则函数-f(x)在R上是减函数函数,结合(1)知:g(x)-f(x)在R上是减函数;
(4)若奇函数f(x)在(0,+∞)上递减,由于奇函数关于原点对称,所以f(x)在(-∞,0)上也递减.
而(3)若函数f(x)在区间[a,b]上递增,在(b,c)上也递增,如图:

可知函数在[-1,1]是增函数,在(1,2)上也是增函数,但不能说函数在[-1,2)为增函数.
故答案为:3.
点评:本题考查的是函数单调性的判断和证明问题.在解答的过程当中充分体现了函数单调性的定义和数形结合的思想.值得同学们体会反思.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目