题目内容
设M是□ABCD的对角线的交点,O为任意一点(且不与M重合),则
+
+
+
等于( )
| OA |
| OB |
| OC |
| OD |
分析:因为此题为单选题,故可考虑用特殊值法去做,因为O为任意一点,不妨把O看成是特殊点,再代入
+
+
+
,计算,结果满足哪一个选项,就选哪一个.
| OA |
| OB |
| OC |
| OD |
解答:解:∵O为任意一点,不妨把A点O看成O点,则
+
+
+
=
+
+
+
,
∵M是□ABCD的对角线的交点,∴
+
+
+
=2
=4
故选D
| OA |
| OB |
| OC |
| OD |
| 0 |
| AB |
| AC |
| AD |
∵M是□ABCD的对角线的交点,∴
| 0 |
| AB |
| AC |
| AD |
| AC |
| AM |
故选D
点评:本题考查了平面向量的加法,做题时应掌握规律,认真解答.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
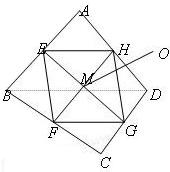 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.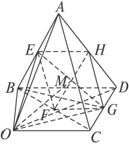
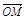 =
= (
( +
+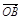 +
+ +
+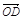 ).
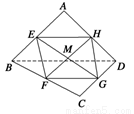
). 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点. .
.