题目内容
如图所示,已知E、F、G、H分别是空间四边形ABCD边AB、BC、CD、DA的中点.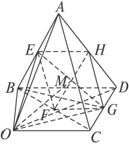
（1）用向量法证明E、F、G、H四点共面；
（2）用向量法证明BD∥平面EFGH；
（3）设M是EG和FH的交点，求证：对空间任一点O，有
=
（
）.
解析:(1)连结BG,则=+
=
+
(
+
)=
+
+
=
+
,
由共面向量定理的推论知E、F、G、H四点共面.
(2)∵
=
-
=
-
=
(
-
)=
,
∴EH∥BD.又EH
面
GH,BD
面EFGH,
∴BD∥平面EFGH.
(3)连结OM、OA、OB、OC、OD、OE、OG,
由(2)知
=
.同理, 
=
.
∴
=
,EH
FG.
∴EG、FH交于一点M且被M平分.
∴
=
(
+
)=
+
=
［
(
+
)］+
［
(
+
)］=
(
+
+
+
).
练习册系列答案
相关题目
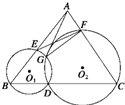如图所示，已知D为△ABC的BC边上一点，⊙O1经过点B，D，交AB于另一点E，⊙O2经过点C，D，交
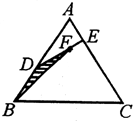如图所示，已知D是面积为1的△ABC的边AB的中点，E是边AC上任一点，连接DE，F是线段DE上一点，连接BF，设，
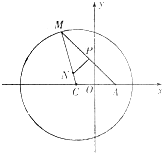如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足AM=2AP，NP⊥AM，点N的轨迹为曲线E．
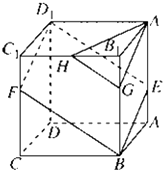如图所示，已知ABCD-A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，G在BB1上，且AE=FC1=B1G=1，H是B1C1的中点．
，则△BEF在△ABD面上的射影是 