题目内容
 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.(1)用向量法证明E,F,G,H(2)四点共面;
(2)用向量法证明:BD∥平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有
 .
.
【答案】分析:(1)用向量的加法求出 ,即可证明E,F,G,H(2)四点共面;
,即可证明E,F,G,H(2)四点共面;
(2)用向量表示 ,就证明EH∥BD,又EH?面EFGH,BD不在 面EFGH,所以BD∥平面EFGH;
,就证明EH∥BD,又EH?面EFGH,BD不在 面EFGH,所以BD∥平面EFGH;
(3)M是EG和FH的交点,利用 推出EG、FH交于一点M且被M平分,然后推出
推出EG、FH交于一点M且被M平分,然后推出 .
.
解答:证明:(1)连接BG,则
 =
=
由共面向量定理的推论知:E、F、G、H四点共面,(其中 )
)
(2)因为 .
.
所以EH∥BD,又EH?面EFGH,BD不在 面EFGH
所以BD∥平面EFGH.
(3)连接OM,OA,OB,OC,OD,OE,OG
由(2)知 ,同理
,同理 ,所以
,所以 ,
,
EH∥FG,EH=FG,所以EG、FH交于一点M且被M平分,
所以
=
点评:本题考查向量语言表述线面的垂直、平行关系,共线向量与共面向量,考查运算能力,是中档题.
 ,即可证明E,F,G,H(2)四点共面;
,即可证明E,F,G,H(2)四点共面;(2)用向量表示
 ,就证明EH∥BD,又EH?面EFGH,BD不在 面EFGH,所以BD∥平面EFGH;
,就证明EH∥BD,又EH?面EFGH,BD不在 面EFGH,所以BD∥平面EFGH;(3)M是EG和FH的交点,利用
 推出EG、FH交于一点M且被M平分,然后推出
推出EG、FH交于一点M且被M平分,然后推出 .
.解答:证明:(1)连接BG,则
 =
=
由共面向量定理的推论知:E、F、G、H四点共面,(其中
 )
)(2)因为
 .
.所以EH∥BD,又EH?面EFGH,BD不在 面EFGH
所以BD∥平面EFGH.
(3)连接OM,OA,OB,OC,OD,OE,OG
由(2)知
 ,同理
,同理 ,所以
,所以 ,
,EH∥FG,EH=FG,所以EG、FH交于一点M且被M平分,
所以

=

点评:本题考查向量语言表述线面的垂直、平行关系,共线向量与共面向量,考查运算能力,是中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
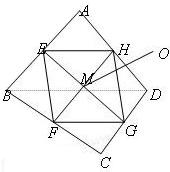 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.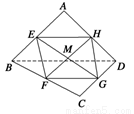
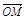 =
= (
( +
+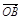 +
+ +
+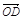 ).
).